
【题目】对于⊙C与⊙C上的一点A,若平面内的点P满足:射线AP与⊙C交于点Q(点Q可以与点P重合),且![]() ,则点P称为点A关于⊙C的“生长点”.
,则点P称为点A关于⊙C的“生长点”.
已知点O为坐标原点,⊙O的半径为1,点A(-1,0).
(1)若点P是点A关于⊙O的“生长点”,且点P在x轴上,请写出一个符合条件的点P的坐标________;
(2)若点B是点A关于⊙O的“生长点”,且满足![]() ,求点B的纵坐标t的取值范围;
,求点B的纵坐标t的取值范围;
(3)直线![]() 与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
【答案】(1)(2,0)(答案不唯一);(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:
(1)由题意可知,在x轴上找点P是比较简单的,这样的P点不是唯一的,如点(2,0)、(1,0)等;
(2)如图1,在x轴上方作射线AM交⊙O于点M,使tan∠MAO=![]() ,并在射线AM是取点N,使MN=AM,则由题意可知,线段MN上的点都是符合条件的B点,过点M作MH⊥x轴于点H,连接MC,结合已知条件求出点M和点N的纵坐标即可得到所求B点的纵坐标t的取值范围;根据对称性,在x轴的下方得到线段M′N′,同理可求得满足条件的B点的纵坐标t的另一取值范围;
,并在射线AM是取点N,使MN=AM,则由题意可知,线段MN上的点都是符合条件的B点,过点M作MH⊥x轴于点H,连接MC,结合已知条件求出点M和点N的纵坐标即可得到所求B点的纵坐标t的取值范围;根据对称性,在x轴的下方得到线段M′N′,同理可求得满足条件的B点的纵坐标t的另一取值范围;
(3)如图2,3,由![]() 与x轴交于点M,与y轴交于点N,可得点M的坐标为
与x轴交于点M,与y轴交于点N,可得点M的坐标为![]() ,点N的坐标为
,点N的坐标为![]() ,由此结合∠OMN的正切函数可求得∠OMN=60°;
,由此结合∠OMN的正切函数可求得∠OMN=60°;
以点D(1,0)为圆心,2为半径作圆⊙D,则⊙D和⊙O相切于点A,由题意可知,点A关于⊙O的“生长点”都在⊙O到⊙D之间的平面内,包括两个圆(但点A除外).
然后结合题意和∠OMN=60°分b>0和b<0两种情况在图2和图3中求出ON1和ON2的长即可得到b的取值范围了.
试题解析:
(1)由题意可知,在x轴上找点P是比较简单的,这样的P点不是唯一的,如点(2,0)、(1,0)等;
(2)如图1,在x轴上方作射线AM,与⊙O交于M,且使得![]() ,并在AM上取点N,使AM=MN,并由对称性,将MN关于x轴对称,得
,并在AM上取点N,使AM=MN,并由对称性,将MN关于x轴对称,得![]() ,则由题意,线段MN和
,则由题意,线段MN和![]() 上的点是满足条件的点B.
上的点是满足条件的点B.
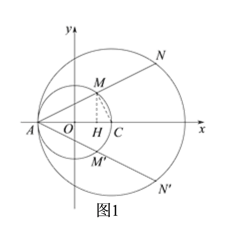
作MH⊥x轴于H,连接MC,
∴ ∠MHA=90°,即∠OAM+∠AMH=90°.
∵ AC是⊙O的直径,
∴ ∠AMC=90°,即∠AMH+∠HMC=90°.
∴ ∠OAM=∠HMC.
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() ,解得
,解得![]() ,即点M的纵坐标为
,即点M的纵坐标为![]() .
.
又由![]() ,A为(-1,0),可得点N的纵坐标为
,A为(-1,0),可得点N的纵坐标为![]() ,
,
故在线段MN上,点B的纵坐标t满足: ![]() .
.
由对称性,在线段![]() 上,点B的纵坐标t满足:
上,点B的纵坐标t满足: ![]() .
.
∴ 点B的纵坐标t的取值范围是![]() 或
或![]() .
.
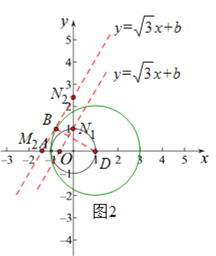
(3)如图2,以点D(1,0)为圆心,2为半径作圆⊙D,则⊙D和⊙O相切于点A,由题意可知,点A关于⊙O的“生长点”都在⊙O到⊙D之间的平面内,包括两个圆(但点A除外).
∵直线![]() 与x轴交于点M,与y轴交于点N,
与x轴交于点M,与y轴交于点N,
∴点M的坐标为![]() ,点N的坐标为
,点N的坐标为![]() ,
,
∴tan∠OMN=![]() ,
,
∴∠OMN=60°,
要在线段MN上找点A关于⊙O的“生长点”,现分“b>0”和“b<0”两种情况讨论:
I、①当直线![]() 过点N1(0,1)时,线段MN上有点A关于⊙O的唯一“生长点”N1,此时b=1;
过点N1(0,1)时,线段MN上有点A关于⊙O的唯一“生长点”N1,此时b=1;
②当直线![]() 与⊙D相切于点B时,线段MN上有点A关于⊙O的唯一“生长点”B,此时直线
与⊙D相切于点B时,线段MN上有点A关于⊙O的唯一“生长点”B,此时直线![]() 与y轴相交于点N2,与x轴相交于点M2,连接DB,则DB=2,
与y轴相交于点N2,与x轴相交于点M2,连接DB,则DB=2,
∴DM2=![]() ,
,
∴OM2=![]() ,
,
∴ON2=tan60°·OM2=![]() ,此时b=
,此时b=![]() .
.
综合①②可得,当b>0时,若线段MN上存在点A关于⊙O的“生长点”,则b的取值范围为: ![]() ;
;
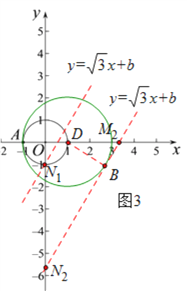
II、当b<0时,如图3,同理可得若线段MN上存在点A关于⊙O的“生长点”,则b的取值范围为: ![]() ;
;
综上所述,若在线段MN上存在点A关于⊙O的“生长点”,则b的取值范围为: ![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图点P是△ABC的边BC上的一动点,点E与点P关于直线AB成轴对称,连接EP交AB于点F,连接AP、EC相交于点O,连接AE.

(1)判断AE与AP的数量关系,并说明理由.
(2)在点P的运动过程中,当AE∥BC时,判断AP与BP的数量关系,并说明理由.
(3)若∠BAC=900,点P在运动过程中是否存在线段AP与线段EC互相平分的情况,若存在,请求出点P的位置;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个少年在绿茵场上游戏.小红从点A出发沿线段AB运动到点B,小兰从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人的运动路线如图1所示,其中AC![]() DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )
DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )


A. 小红的运动路程比小兰的长
B. 两人分别在1.09秒和7.49秒的时刻相遇
C. 当小红运动到点D的时候,小兰已经经过了点D
D. 在4.84秒时,两人的距离正好等于⊙O的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图,探究:
(1)一个正方体组合图形的主视图、左视图(如图1)所示.
①这个几何体可能是(图2)甲、乙中的 ;
②这个几何体最多可由 个小正方体构成,请在图3中画出符合最多情况的一个俯视图.
(2)如图,已知一平面内的四个点A、B、C、D,根据要求用直尺画图.
①画线段AB,射线AD;
②找一点M,使M点即在射线AD上,又在直线BC上;
③找一点N,使N到A、B、C、D四个点的距离和最短.


查看答案和解析>>
科目:初中数学 来源: 题型:
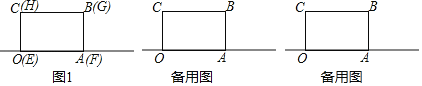
【题目】有两个大小完全一样的长方形OABC和EFGH重合放在一起,边OA、EF在数轴上,O为数轴原点(如图1),长方形OABC的边长OA的长为6个坐标单位.
(1)数轴上点A表示的数为 .
(2)将长方形EFGH沿数轴所在直线水平移动
①若移动后的长方形EFGH与长方形OABC重叠部分的面积恰好等于长方形OABC面积的![]() ,则移动后点F在数轴上表示的数为 .
,则移动后点F在数轴上表示的数为 .
②若出行EFGH向左水平移动后,D为线段AF的中点,求当长方形EFGH移动距离x为何值时,D、E两点在数轴上表示的数是互为相反数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从(0,2)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2019次碰到矩形的边时点P的坐标为( )
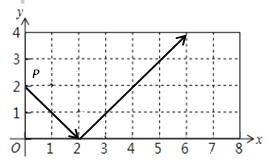
A.( 2,4 )B.( 2,0 )C.( 8,2)D.( 6,0 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取900°;而乙同学说,θ也能取800°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com