
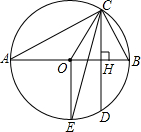
 的中点,连接0E,CE.求证:CE平分∠OCD.
的中点,连接0E,CE.求证:CE平分∠OCD. 的中点,根据垂径定理的推论得OE⊥AB,则OE∥CD,根据平行线的性质得∠OEC=∠ECD,而∠OEC=∠OCE,所以∠OCE=∠ECD;
的中点,根据垂径定理的推论得OE⊥AB,则OE∥CD,根据平行线的性质得∠OEC=∠ECD,而∠OEC=∠OCE,所以∠OCE=∠ECD; OA=2,则GF=OG-OF=2,于是可得到在弧AC上没有一个点到AC的距离为3cm,在弧AEC上有两个点到AC的距离为3cm.
OA=2,则GF=OG-OF=2,于是可得到在弧AC上没有一个点到AC的距离为3cm,在弧AEC上有两个点到AC的距离为3cm. 的中点,
的中点,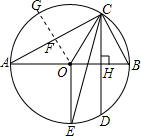
 OA=2,
OA=2, 上到AC的最大距离为2cm,
上到AC的最大距离为2cm, 上没有一个点到AC的距离为3cm,
上没有一个点到AC的距离为3cm, 上到AC的最大距离为6cm,
上到AC的最大距离为6cm, 上有两个点到AC的距离为3cm.
上有两个点到AC的距离为3cm.

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,M是弧AB的中点,OC⊥OD,△COD绕点O旋转与△AMB的两边分别交于E、F(点E、F与点A、B、M均不重合),与⊙O分别交于P、Q两点.
,M是弧AB的中点,OC⊥OD,△COD绕点O旋转与△AMB的两边分别交于E、F(点E、F与点A、B、M均不重合),与⊙O分别交于P、Q两点.
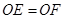 ;
;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com