
【题目】如图,四边形ABCD、DEFG都是正方形,边长分别为m、n(m<n).坐标原点O为AD的中点,A、D、E在y轴上.若二次函数y=ax2的图象过C、F两点,则![]() =_____.
=_____.

科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O是直线AB上一点,OD是∠AOC的平分线,∠COD与∠COE互余
求证:∠AOE与∠COE互补.

请将下面的证明过程补充完整:
证明:∵O是直线AB上一点
∴∠AOB=180°
∵∠COD与∠COE互余
∴∠COD+∠COE=90°
∴∠AOD+∠BOE=_________°
∵OD是∠AOC的平分线
∴∠AOD=∠________(理由:_______________)
∴∠BOE=∠COE(理由:________________)
∵∠AOE+∠BOE=180°
∴∠AOE+∠COE=180°
∴∠AOE与∠COE互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,A(﹣3,0),B(1,b),则正方形ABCD的面积为( )
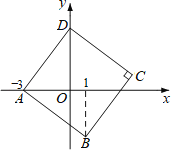
A.34B.25C.20D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正五边形与一个正方形的边长正好相等,在它们相接的地方,形成一个完整的“苹果”图案(如图).如果让正方形沿着正五边形的四周滚动,并且始终保持正方形和正五边形有两条边邻接,那么第一次恢复“苹果”的图形时,正方形要绕五边形转( )圈.
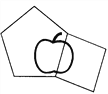
A. 4 B. 3 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善教室空气环境,某校九年级1班班委会计划到朝阳花卉基地购买绿植.已知该基地一盆绿萝与一盆吊兰的价格之和是12元.班委会决定用60元购买绿萝,用90元购买吊兰,所购绿萝数量正好是吊兰数量的两倍.
(1)分别求出每盆绿萝和每盆吊兰的价格;
(2)该校九年级所有班级准备一起到该基地购买绿萝和吊兰共计90盆,其中绿萝数量不超过吊兰数量的一半,该基地特地对吊兰价格给出了如下的优惠政策,一次性购买的吊兰超过20盆时,超过部分的吊兰每盆的价格打8折,根据该基地的优惠信息,九年级购买这两种绿植各多少盆时总费用最少?最少费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com