
ЁОЬтФПЁПжБНЧШ§НЧаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌжБЯп
ЃЌжБЯп![]() Й§Еу
Й§Еу![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌШчЭМ1ЃЌЗжБ№Й§Еу
ЪБЃЌШчЭМ1ЃЌЗжБ№Й§Еу![]() КЭ
КЭ![]() зї
зї![]() жБЯп
жБЯп![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() жБЯп
жБЯп![]() гкЕу
гкЕу![]() .
.![]() гы
гы![]() ЪЧЗёШЋЕШЃЌВЂЫЕУїРэгЩЃЛ
ЪЧЗёШЋЕШЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌШчЭМ2ЃЌЕу
ЪБЃЌШчЭМ2ЃЌЕу![]() гыЕу
гыЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЖдГЦЃЌСЌНг
ЖдГЦЃЌСЌНг![]() ЁЂ
ЁЂ![]() .Еу
.Еу![]() ЪЧ
ЪЧ![]() ЩЯвЛЕуЃЌЕу
ЩЯвЛЕуЃЌЕу![]() ЪЧ
ЪЧ![]() ЩЯвЛЕуЃЌЗжБ№Й§Еу
ЩЯвЛЕуЃЌЗжБ№Й§Еу![]() ЁЂ
ЁЂ![]() зї
зї![]() жБЯп
жБЯп![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() жБЯп
жБЯп![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() Дг
Дг![]() ЕуГіЗЂЃЌвдУПУы
ЕуГіЗЂЃЌвдУПУы![]() ЕФЫйЖШби
ЕФЫйЖШби![]() ТЗОЖдЫЖЏЃЌжеЕуЮЊ
ТЗОЖдЫЖЏЃЌжеЕуЮЊ![]() .Еу
.Еу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдУПУы
ГіЗЂЃЌвдУПУы![]() ЕФЫйЖШби
ЕФЫйЖШби![]() ТЗОЖдЫЖЏЃЌжеЕуЮЊ
ТЗОЖдЫЖЏЃЌжеЕуЮЊ![]() .Еу
.Еу![]() ЁЂ
ЁЂ![]() ЭЌЪБПЊЪМдЫЖЏЃЌИїздДяЕНЯргІЕФжеЕуЪБЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ
ЭЌЪБПЊЪМдЫЖЏЃЌИїздДяЕНЯргІЕФжеЕуЪБЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ![]() Уы.
Уы.
ЂйЕБ![]() ЮЊЕШбќжБНЧШ§НЧаЮЪБЃЌЧѓ
ЮЊЕШбќжБНЧШ§НЧаЮЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкЕБ![]() гы
гы![]() ШЋЕШЪБЃЌЧѓ
ШЋЕШЪБЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.


ЭМ1 ЭМ2
ЁОД№АИЁП(1)ЁїACDЁеЁїCBE.
(2)Ђй![]() Лђ5. ЂкЕБt=3.5УыЛђ5УыЛђ6.5УыЪБ,ЁїMDCЁеЁїCEN.
Лђ5. ЂкЕБt=3.5УыЛђ5УыЛђ6.5УыЪБ,ЁїMDCЁеЁїCEN.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЭЌНЧЕФгрНЧЯрЕШЕУЕНЁЯDAC=ЁЯECBЃЌИљОнШЋЕШШ§НЧаЮЕФХаЖЈЖЈРэжЄУїМДПЩЃЛ
ЃЈ2ЃЉЂйЗжЕуNбиFЁњCЁњBТЗОЖдЫЖЏЁЂЕуNбиBЁњCТЗОЖдЫЖЏСНжжЧщПіНјааЬжТл.
ЂкЗжЕуNбиFЁњCТЗОЖдЫЖЏЁЂЕуNбиCЁњBТЗОЖдЫЖЏЁЂЕуNбиBЁњCТЗОЖдЫЖЏЁЂЕуNбиCЁњFТЗОЖдЫЖЏЫФжжЧщПіМЦЫуМДПЩЃЎ
(1)ЁїACDЁеЁїCBEЃЌ
РэгЩШчЯТЃКЁп![]()
Ёр![]()
ЁпADЁЭжБЯпlЃЌ
Ёр![]()
ЁрЁЯDAC=ЁЯECBЃЌ
дкЁїACDКЭЁїCBEжаЃЌ
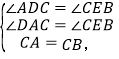
ЁрЁїACDЁеЁїCBEЃЛ
(2)ЂйЕБ![]() ЮЊЕШбќжБНЧШ§НЧаЮЪБЃЌЕуNдкBCЩЯЃЌ
ЮЊЕШбќжБНЧШ§НЧаЮЪБЃЌЕуNдкBCЩЯЃЌ
![]()
Еу![]() ДгЕу
ДгЕу![]() ГіЗЂЕквЛДЮЕНЯпЖЮCBЩЯЪБЃЌ
ГіЗЂЕквЛДЮЕНЯпЖЮCBЩЯЪБЃЌ
![]()
![]()
![]() НтЬт
НтЬт![]()
Еу![]() ДгЕу
ДгЕу![]() ГіЗЂЕкЖўДЮЕНЯпЖЮCBЩЯЪБЃЌ
ГіЗЂЕкЖўДЮЕНЯпЖЮCBЩЯЪБЃЌ
![]()
![]()
![]() НтЬт
НтЬт![]()
ЂкгЩЬтвтЕУЃЌCF=BC=6cmЃЌ
гЩ(1)ЕУЃЌЁЯDAC=ЁЯECBЃЌЁЯADC=ЁЯCEBЃЌ
ЁрЕБCM=CNЪБ,ЁїMDCЁеЁїCENЃЌ
ЕБЕуNбиFЁњCТЗОЖдЫЖЏЪБЃЌ8t=63tЃЌ
НтЕУЃЌt=1ЃЌВЛКЯЬтвтЃЌ
ЕБЕуNбиCЁњBТЗОЖдЫЖЏЪБЃЌ8t=3t6ЃЌ
НтЕУЃЌt=3.5ЃЌ
ЕБЕуNбиBЁњCТЗОЖдЫЖЏЪБЃЌ8t=3t12ЃЌ
НтЕУЃЌt=5ЃЌ
ЕБЕуNбиCЁњFТЗОЖдЫЖЏЪБЃЌ8t=3t18ЃЌ
НтЕУЃЌt=6.5ЃЌ
злЩЯЫљЪі,ЕБt=3.5УыЛђ5УыЛђ6.5УыЪБ,ЁїMDCЁеЁїCEN.


 ШЪАЎгЂгяЭЌВНСЗЯАВсЯЕСаД№АИ
ШЪАЎгЂгяЭЌВНСЗЯАВсЯЕСаД№АИ бЇЯАЪЕМљдАЕиЯЕСаД№АИ
бЇЯАЪЕМљдАЕиЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫГДЮСЌНгБпГЄЮЊ1ЕФе§ЗНаЮABCDЫФБпЕФжаЕуЃЌЕУЕНЫФБпаЮA1B1C1D1 ЃЌ ШЛКѓЫГДЮСЌНгЫФБпаЮA1B1C1D1ЫФБпЕФжаЕуЃЌЕУЕНЫФБпаЮA2B2C2D2 ЃЌ дйЫГДЮСЌНгЫФБпаЮA2B2C2D2ЫФБпЕФжаЕуЃЌЕУЕНЫФБпаЮA3B3C3D3 ЃЌ ЁЃЌАДДЫЗНЗЈЕУЕНЕФЫФБпаЮA8B8C8D8ЕФжмГЄЮЊ ЃЎ 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉвбжЊвЛдЊЖўДЮЗНГЬax2+bx+c=0ЃЈaЁй0ЃЉгаСНИљx1 ЃЌ x2ЃЈb2Љ4acЁн0ЃЉЃЎгУЧѓИљЙЋЪНаДГіx1 ЃЌ x2 ЃЌ ВЂжЄУїx1+x2=Љ ![]() ЃЌx1x 2=
ЃЌx1x 2= ![]()
ЃЈ2ЃЉШєвЛдЊЖўДЮЗНГЬx2+xЉ1=0ЕФСНИљЮЊmЃЌnЃЌдЫгУЃЈ1ЃЉжаЕФНсТлЃЌЧѓ ![]() +
+ ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌНЋЁїABOШЦЕуAЫГЪБеыа§зЊЕНЁїAB1C1ЕФЮЛжУЃЌЕуBЁЂOЗжБ№ТфдкЕуB1ЁЂC1ДІЃЌЕуB1дкxжсЩЯЃЌдйНЋЁїAB1C1ШЦЕуB1ЫГЪБеыа§зЊЕНЁїA1B1C2ЕФЮЛжУЃЌЕуC2дкxжсЩЯЃЌНЋЁїA1B1C2ШЦЕуC2ЫГЪБеыа§зЊЕНЁїA2B2C2ЕФЮЛжУЃЌЕуA2дкxжсЩЯЃЌвРДЮНјааЯТШЅЁЃЎШєЕуAЃЈ3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЌдђЕуB100ЕФзјБъЮЊ ЃЎ 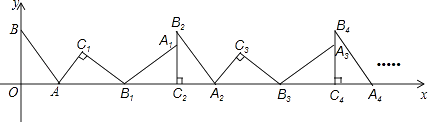
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
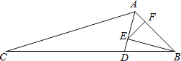
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЮЊ
ЮЊ![]() ЦНЗжЯпЃЌ
ЦНЗжЯпЃЌ![]() гк
гк![]() ЃЌ
ЃЌ![]() гк
гк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ________ЃЎ
________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНУцжБНЧзјБъЯЕжаЃЌвбжЊAЃЈ8ЃЌ0ЃЉЃЌЁїAOPЮЊЕШбќШ§НЧаЮЧвУцЛ§ЮЊ16ЃЌТњзуЬѕМўЕФPЕугаЃЈЁЁЁЁЃЉ
A. 4Иі B. 8Иі C. 10Иі D. 12Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьвдЯТЕШЪНЃК
Ек1ИіЕШЪНЃК![]() +
+![]() +
+![]() ЁС
ЁС![]() =1ЃЌ
=1ЃЌ
Ек2ИіЕШЪНЃК![]() +
+![]() +
+![]() ЁС
ЁС![]() =1ЃЌ
=1ЃЌ
Ек3ИіЕШЪНЃК![]() +
+![]() +
+![]() ЁС
ЁС![]() =1ЃЌ
=1ЃЌ
Ек4ИіЕШЪНЃК![]() +
+![]() +
+![]() ЁС
ЁС![]() =1ЃЌ
=1ЃЌ
Ек5ИіЕШЪНЃК![]() +
+![]() +
+![]() ЁС
ЁС![]() =1ЃЌ
=1ЃЌ
ЁЁ
АДеевдЩЯЙцТЩЃЌНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉаДГіЕк6ИіЕШЪНЃК_____ЃЛ
ЃЈ2ЃЉаДГіФуВТЯыЕФЕкnИіЕШЪНЃК_____ЃЈгУКЌnЕФЕШЪНБэЪОЃЉЃЌВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌгаЯТСа4ИіНсТлЃКЂйabcЃО0ЃЛЂкbЃМa+cЃЛЂл4a+2b+cЃО0ЃЛЂмb2Љ4acЃО0ЃЛЦфжае§ШЗЕФНсТлгаЃЈ ЃЉ 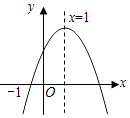
A.1Иі
B.2Иі
C.3Иі
D.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаМзЁЂввЁЂБћШ§жжЬЧЙћЛьКЯЖјГЩЕФЪВНѕЬЧ100ЧЇПЫЃЌЦфжаИїжжЬЧЙћЕФЕЅМлКЭЧЇПЫЪ§ШчБэЫљЪОЃЌЩЬМвгУМгШЈЦНОљЪ§РДШЗЖЈЪВНѕЬЧЕФЕЅМлЃЎ
МзжжЬЧЙћ | ввжжЬЧЙћ | БћжжЬЧЙћ | |
ЕЅМлЃЈдЊ/ЧЇПЫЃЉ | 15 | 25 | 30 |
ЧЇПЫЪ§ | 40 | 40 | 20 |
ЃЈ1ЃЉЧѓИУЪВНѕЬЧЕФЕЅМлЃЎ
ЃЈ2ЃЉЮЊСЫЪЙЪВНѕЬЧЕФЕЅМлУПЧЇПЫжСЩйНЕЕЭ2дЊЃЌЩЬМвМЦЛЎдкЪВНѕЬЧжаМгШыМзЁЂБћСНжжЬЧЙћЙВ100ЧЇПЫЃЌЮЪЦфжазюЖрПЩМгШыБћжжЬЧЙћЖрЩйЧЇПЫЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com