
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E. 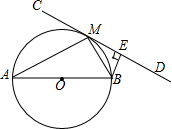
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE= ![]() ,sin∠BAM=
,sin∠BAM= ![]() ,求线段AM的长.
,求线段AM的长.
【答案】
(1)证明:如图,连接OM,
∵直线CD切⊙O于点M,
∴∠OMD=90°,
∴∠BME+∠OMB=90°,
∵AB为⊙O的直径,
∴∠AMB=90°.
∴∠AMO+∠OMB=90°,
∴∠BME=∠AMO,
∵OA=OM,
∴∠MAB=∠AMO,
∴∠BME=∠MAB

(2)证明:由(1)有,∠BME=∠MAB,
∵BE⊥CD,
∴∠BEM=∠AMB=90°,
∴△BME∽△BAM,
∴ ![]() ,
,
∴BM2=BEAB
(3)解:由(1)有,∠BME=∠MAB,
∵sin∠BAM= ![]() ,
,
∴sin∠BME= ![]() ,
,
在Rt△BEM中,BE= ![]() ,
,
∴sin∠BME= ![]() =
= ![]() ,
,
∴BM=6,
在Rt△ABM中,sin∠BAM= ![]() ,
,
∴sin∠BAM= ![]() =
= ![]() ,
,
∴AB= ![]() BM=10,
BM=10,
根据勾股定理得,AM=8
【解析】(1)由切线的性质得出∠BME+∠OMB=90°,再由直径得出∠AMB=90°,利用同角的余角相等判断出结论;(2)由(1)得出的结论和直角,判断出△BME∽△BAM,即可得出结论,(3)先在Rt△BEM中,用三角函数求出BM,再在Rt△ABM中,用三角函数和勾股定理计算即可.


科目:初中数学 来源: 题型:
【题目】(本题6分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(2,2),B(4,1),C(4,4).
(1)作出 ![]() ABC关于原点O成中心对称的
ABC关于原点O成中心对称的 ![]() A1B1C1.
A1B1C1.
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 ![]() A1B1C1的内部(不包括顶点和边界),求a的取值范围.
A1B1C1的内部(不包括顶点和边界),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的括号内:
-11,![]() ,3,
,3,![]() ,0,
,0,![]() ,
,![]() ,-12.101001…,-π,0.4.
,-12.101001…,-π,0.4.
有理数{ …};
无理数{ ……};
正实数{ …};
负实数{ ……}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
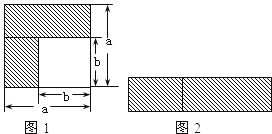
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
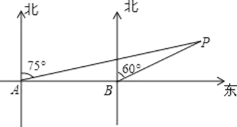
【题目】如图,某轮船由西向东航行,在 A 处测得小岛 P 的方位是北偏东 75°,又继续航行 8 海里后,在 B 处测得小岛 P 的方位是北偏东 60°,则此时△ABP 的面积为______平方海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
课题 | 测量教学楼高度 | |
方案 | 一 | 二 |
图示 |
|
|
测得数据 | CD=6.9m,∠ACG=22°,∠BCG=13°, | EF=10m,∠AEB=32°,∠AFB=43° |
参考数据 | sin22°≈0.37,cos22°≈0.93, | sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 |
请你选择其中的一种方法,求教学楼的高度(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
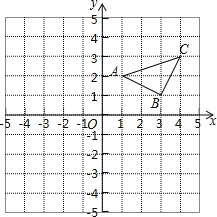
【题目】已知:如图,在平面直角坐标系中,
(1) 作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标:
A1 ,B1 ,C1 .
(2) 直接写出△ABC的面积为 .
(3) 在x轴上画点P,使△PAC的周长最小. (不写作法,保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.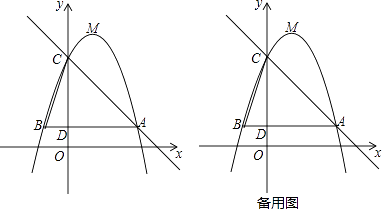
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com