
分析 (1)把n的值分别代入$\frac{(n-2)•180°}{n}$进行计算即可;
(2)①由观察图形可以看出∠APD是△APB的一个外角,∠APD=∠BAE+∠ABD.又可得出△ABE≌△BCD,由此便可求出∠APD的度数,∠APD=∠ABP+∠BAE=∠ABP+∠CBD=∠ABE=60°;∠APD易证等于∠M,即等于多边形的内角.
②点E、D分别是正n边形ABCM中以C点为顶点的相邻两边上的点,且BE=CD,BD与AE交于点P,∠APD等于正n边形的内角,就可以求出.
解答  解:(1)正三角形的每个内角是:$\frac{(3-2)•180°}{3}$=60°;
解:(1)正三角形的每个内角是:$\frac{(3-2)•180°}{3}$=60°;
正四边形的每个内角是:$\frac{(4-2)•180°}{4}$=90°;
正五边形的每个内角是:$\frac{(5-2)•180°}{5}$=108°.
故答案是:60;90;108;
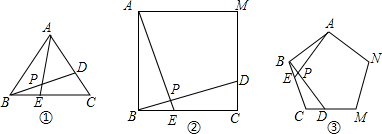
(2)①如图①,∠APD=60°,理由如下:
∵△ABC是等边三角形,
∴AB=BC,∠ABE=∠BCD=60°.
∵在△ABE与△BCD中,$\left\{\begin{array}{l}{BE=CD}\\{∠ABE=∠BCD=60°}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCD(SAS).
∴∠BAE=∠CBD.
∴∠APD=∠ABP+∠BAE=∠ABP+∠CBD=∠ABE=60°.
如图②,∠APD=90°,理由如下:
同理可证:△ABE≌△BCD,
∴∠AEB+∠DBC=180°-90°=90°,
∴∠APD=∠BPE=180°-90°=90°;
如图③,∠APD=108°,理由如下: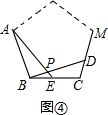
同理可证:△ABE≌△BCD,
∴∠AEB+∠DBC=180°-108°=72°,
∴∠APD=∠BPE=180°-(∠AEB+∠DBC)=180°-72°=108°.
②能.如图④,点E、D分别是正n边形ABCM中以C点为顶点的相邻两边上的点,且BE=CD,BD与AE交于点P,则∠APD的度数为$\frac{(n-2)•180°}{n}$.
点评 此题主要考查了四边形综合题,此题应当根据正多边形的性质证明一对全等三角形,再结合三角形的外角的性质,发现要求的角总等于正多边形的一个内角.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 全球通 | 神州行 | |
| 月租费 | 15元/月 | 0 |
| 本地通话费 | 0.10元/分 | 0.20元/分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8.5×104 | B. | 8.5×105 | C. | 0.85×104 | D. | 0.85×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com