
分析 (1)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可;
(2)根据同底数幂的除法法则进行计算即可.
解答 解:(1)原式=[$\frac{x+1}{(x+1)(x-1)}$+$\frac{x}{x-1}$]÷$\frac{x+1}{(x-1)^{2}}$
=[$\frac{1}{x-1}$+$\frac{x}{x-1}$]•$\frac{(x-1)^{2}}{x+1}$
=$\frac{x+1}{x-1}$•$\frac{{(x-1)}^{2}}{x+1}$
=x-1,
当x=2时,原式=1;
(2)∵xm=6,xn=3,
∴x2m-3n=$\frac{{x}^{2m}}{{x}^{3n}}$=$\frac{({x}^{m})^{2}}{({x}^{n})^{3}}$=$\frac{{6}^{2}}{{3}^{3}}$=$\frac{36}{27}$=$\frac{4}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:填空题
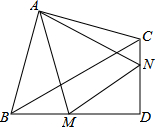 如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=8,AB=AC,∠CBD=30°,BD=4$\sqrt{3}$,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为4$\sqrt{3}$+4.
如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=8,AB=AC,∠CBD=30°,BD=4$\sqrt{3}$,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为4$\sqrt{3}$+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com