
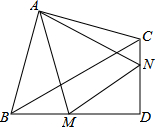
 如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=8,AB=AC,∠CBD=30°,BD=4$\sqrt{3}$,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为4$\sqrt{3}$+4.
如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=8,AB=AC,∠CBD=30°,BD=4$\sqrt{3}$,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为4$\sqrt{3}$+4. 分析 将△ACN绕点A逆时针旋转,得到△ABE,由旋转得出∠NAE=90°,AN=AE,∠ABE=∠ACD,∠EAB=∠CAN,求出∠EAM=∠MAN,根据SAS推出△AEM≌△ANM,根据全等得出MN=ME,求出MN=CN+BM,解直角三角形求出DC,即可求出△DMN的周长=BD+DC,代入求出即可.
解答 解:将△ACN绕点A逆时针旋转,得到△ABE,如图: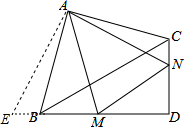
由旋转得:∠NAE=90°,AN=AE,∠ABE=∠ACD,∠EAB=∠CAN,
∵∠BAC=∠D=90°,
∴∠ABD+∠ACD=360°-90°-90°=180°,
∴∠ABD+∠ABE=180°,
∴E,B,M三点共线,
∵∠MAN=45°,∠BAC=90°,
∴∠EAM=∠EAB+∠BAM=∠CAN+∠BAM=∠BAC-∠MAN=90°-45°=45°,
∴∠EAM=∠MAN,
在△AEM和△ANM中,
$\left\{\begin{array}{l}{AE=AN}\\{∠EAM=∠NAM}\\{AM=AM}\end{array}\right.$,
∴△AEM≌△ANM(SAS),
∴MN=ME,
∴MN=CN+BM,
∵在Rt△BCD中,∠BDC=90°,∠CBD=30°,BD=4$\sqrt{3}$,CD=BD×tan∠CBD=4,
∴△DMN的周长为DM+DN+MN=DM+DN+BM+CN=BD+DC=4$\sqrt{3}$+4,
故答案为:4$\sqrt{3}$+4.
点评 本题考查了解直角三角形,全等三角形的性质和判定,旋转的性质的应用,能正确作出辅助线是解此题的关键.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
 作图题
作图题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校举行一次数学知识竞赛,任选10名参赛学生的成绩并划分等级,制作成如下统计表和扇形统计图
某学校举行一次数学知识竞赛,任选10名参赛学生的成绩并划分等级,制作成如下统计表和扇形统计图 | 编号 | 成绩 | 等级 | 编号 | 成绩 | 等级 |
| ① | 90 | A | ⑥ | 76 | B |
| ② | 78 | B | ⑦ | 85 | A |
| ③ | 72 | C | ⑧ | 82 | B |
| ④ | 79 | B | ⑨ | 77 | B |
| ⑤ | 92 | A | ⑩ | 69 | C |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com