
(本小题满分9分)如图,在矩形ABCD中,E是CD边上一动点,设DE=x,作AF⊥AE交CB的延长线于点F.

(1)当点E不与点C,D重合时,求证:△ADE∽△ABF;
(2)连接EF,M为EF的中点,AB=4,AD=2, 当点E从D运动到C的过程中
①点M经过的路径是( )
A. 直线 B. 线段 C. 射线 D. 圆弧
②求点M经过的路径的长;
③连接BM,直接写出BM的长度的最小值.
【解析】
试题分析:(1)根据矩形得出∠D=∠ABF=90°,根据垂直得出∠DAE=∠BAF,从而说明全等;(2)首先画出极端的两种情况,再看点M的位置关系;我们首先设DE=x,取CF的中点H,连接MH,BM,根据△ADE∽△ABF,得出BF=2x,FC=2+2x,FH=1+x,根据直角△MHB的勾股定理得出BM的二次函数关系式,然后根据二次函数的性质进行求解.
试题解析:(1)∵在矩形ABCD中,∠DAB=∠ABC=∠C=∠D=90°, ∴∠ABF=∠D=90°,
∵AF⊥AE, ∴∠EAF=∠BAF+∠EAB=90°, ∵∠DAE+∠EAB=∠DAB=90°, ∴∠DAE=∠BAF,
∴△ADE∽△ABF;
(2)①、B ②、点M所运动的路程长度等于矩形的对角线长度,则点M运动的长度=2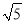
③、BM的最小值为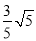
考点:三角形相似的应用
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,△ABC中,DE∥BC,DE=2.2,AD=2,DB=3,则BC的长是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级下学期第一次质量检测数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,抛物线y=ax 2+bx+4经过A(-3,0)、B(4,0)两点,且与y轴交于点C,D(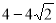 ,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
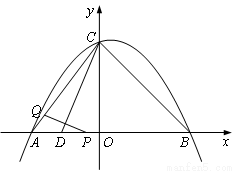
(1)求该抛物线的解析式;
(2)若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;
(3)在第一象限的抛物线上取一点G,使得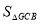 =
=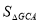 ,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级下学期第一次质量检测数学试卷(解析版) 题型:填空题
如图,将△ABC绕点A逆时针方向旋转到△ADE的位置,点B落在AC边上的点D处,设旋转角为 (0<<90).若B=125,E=30,则= °.
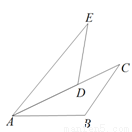
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级下学期第一次质量检测数学试卷(解析版) 题型:选择题
如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD
的度数为( )

A.27° B.54° C.63° D.36°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省丹阳市十乡九年级下学期第一次联考数学试卷(解析版) 题型:解答题
(本小题满分6分)若等腰△ABC的一边长为a=2,另外两边长b、c恰好是关于x的一元二次方程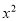 -(m+3)x+m+2=0的两个根,求△ABC的周长.
-(m+3)x+m+2=0的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市九年级上学期期末检测数学试卷(解析版) 题型:解答题
(8分)如图,在△ABC中,D是BC的垂直平分线DH上一点,DF⊥AB于F,DE⊥AC交AC的延长线于E,且BF=CE.
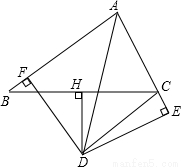
(1)求证:AD平分∠BAC;
(2)若∠BAC=80°,求∠DCB的度数.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省邯郸市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
某篮球队12名队员的年龄如下表所示:
年龄(岁) | 18 | 19 | 20 | 21 |
人数 | 5 | 4 | 1 | 2 |
则这12名队员年龄的众数和中位数分别是( )
A.18,19 B.18,19.5 C.5,4 D.5, 4.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com