
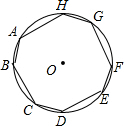
 如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )
如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )| A. | 120° | B. | 125° | C. | 130° | D. | 135° |
分析 连结OA、OG、AD、GD,如图,根据圆心角、弧、弦的关系得到$\widehat{AB}$=$\widehat{CD}$=$\widehat{EF}$=$\widehat{HG}$,$\widehat{BC}$=$\widehat{DE}$=$\widehat{FG}$=$\widehat{AH}$,则$\widehat{AH}$+$\widehat{HG}$=$\widehat{AB}$+$\widehat{BC}$=$\widehat{CD}$+$\widehat{DE}$=$\widehat{EF}$+$\widehat{GF}$,所以∠AOG=90°,然后根据圆周角定理计算出∠ADG=45°,再利用圆内接四边形的性质求∠AHG.
解答 解: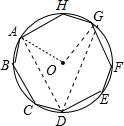 连结OA、OG、AD、GD,如图,
连结OA、OG、AD、GD,如图,
∵AB=CD=EF=HG,BC=DE=FG=AH,
∴$\widehat{AB}$=$\widehat{CD}$=$\widehat{EF}$=$\widehat{HG}$,$\widehat{BC}$=$\widehat{DE}$=$\widehat{FG}$=$\widehat{AH}$,
∴$\widehat{AH}$+$\widehat{HG}$=$\widehat{AB}$+$\widehat{BC}$=$\widehat{CD}$+$\widehat{DE}$=$\widehat{EF}$+$\widehat{GF}$,
即$\widehat{AH}$+$\widehat{HG}$为圆周的$\frac{1}{4}$,
∴∠AOG=360°×$\frac{1}{4}$=90°,
∴∠ADG=$\frac{1}{2}$∠AOG=45°,
∴∠AHG=180°-∠ADG=180°-45°=135°.
故选D.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了圆周角定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 0<d<4 | B. | d>10 | C. | 0≤d<4或d>10 | D. | 4<d<10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
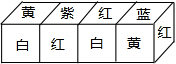 把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:
把正方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花的朵数的情况如下表:| 颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
| 花的朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
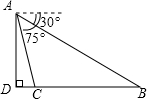 如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )
如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )| A. | 300($\sqrt{3}$+1)m | B. | 1200($\sqrt{3}$-1)m | C. | 1800($\sqrt{3}$-1)m | D. | 2400($\sqrt{2}$-1)m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com