
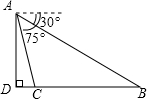
 如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )
如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )| A. | 300($\sqrt{3}$+1)m | B. | 1200($\sqrt{3}$-1)m | C. | 1800($\sqrt{3}$-1)m | D. | 2400($\sqrt{2}$-1)m |
分析 由题意画出图形,由两角差的正切求出15°的正切值,然后通过解两个直角三角形得到DC,DB的长度,作差后可得结果.
解答 解:由已知条件得∠DAB=15°,
∵tan15°=tan(45°-30°)=$\frac{tan45°-tan30°}{1+tan45°tan30°}$=2-$\sqrt{3}$,
在Rt△ADB中,AD=600,
∴DB=AD•tan15°=600×(2-$\sqrt{3}$)=1200-600$\sqrt{3}$,
在Rt△ADC中,AD=600,∠DAC=60°,
∴DC=AD•tan60°=600$\sqrt{3}$,
∴BC=CD-BD=600$\sqrt{3}$-(1200-600$\sqrt{3}$)=1200($\sqrt{3}$-1),
∴长江的宽度BC等于1200($\sqrt{3}$-1).
故选B.
点评 本题考查了解直角三角形的应用;利用三角函数值得到与所求线段相关线段的长度是解决本题的关键.


科目:初中数学 来源: 题型:解答题
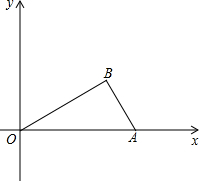 如图,在平面直角坐标系中,Rt△ABO的斜边OA在x轴上,点B在第一象限内,AO=4,∠BOA=30°.点C(t,0)是x轴正半轴上一动点(t>0且t≠4):
如图,在平面直角坐标系中,Rt△ABO的斜边OA在x轴上,点B在第一象限内,AO=4,∠BOA=30°.点C(t,0)是x轴正半轴上一动点(t>0且t≠4):查看答案和解析>>
科目:初中数学 来源: 题型:选择题
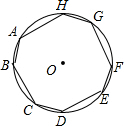 如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )
如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )| A. | 120° | B. | 125° | C. | 130° | D. | 135° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
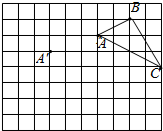 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
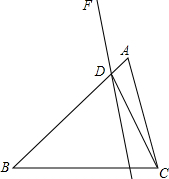 如图,已知△ABC,D为AB边上一点,∠BDC=∠ACB,过点D作直线DF.
如图,已知△ABC,D为AB边上一点,∠BDC=∠ACB,过点D作直线DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,D,E两点分别在AB,AC边上,且DE∥BC,如果$\frac{AD}{AB}=\frac{2}{3}$,AC=6,那么AE的长为( )
如图,△ABC中,D,E两点分别在AB,AC边上,且DE∥BC,如果$\frac{AD}{AB}=\frac{2}{3}$,AC=6,那么AE的长为( )| A. | 3 | B. | 4 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
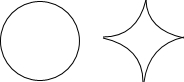 如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )| A. | $\frac{4-π}{π}$ | B. | $\frac{{\sqrt{2}}}{π}$ | C. | $\frac{π-1}{π}$ | D. | $\frac{3}{π}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com