
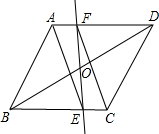
 如图,在?ABCD中,O是对角线BD的中点,过O点的一条直线分别与BC相交于E,与AD相交于F,求证:四边形AECF是平行四边形.
如图,在?ABCD中,O是对角线BD的中点,过O点的一条直线分别与BC相交于E,与AD相交于F,求证:四边形AECF是平行四边形. 分析 通过全等三角形(△FOD≌△EOB)的对应边相等易得FD=EB,则由相关线段间的和差关系得到AF=CE,所以根据“有一组对边平行且相等”的判定定理证得结论即可.
解答 证明:∵ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠FDO=∠EBO.
又∵O是BD的中点,EF过O点,
∴OD=OB,∠FOD=∠EOB.
∴在△FOD与△EOB中,$\left\{\begin{array}{l}{∠FOD=∠EOB}\\{DO=OB}\\{∠FDO=∠EBO}\end{array}\right.$,
∴△FOD≌△EOB(ASA),
∴FD=EB,
∴AF=AD-FD=BC-EB=CE,即有AF∥CE且AF=CE,
∴四边形AECF是平行四边形.(用其他方法证明的,如利用平行四边形的中心对称性质证明的,参照给分)
点评 本题考查了全等三角形的判定与性质,平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
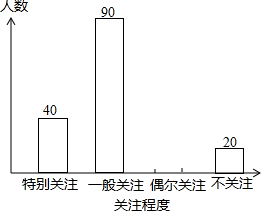 第33届“中国洛阳牡丹文化节”于2015年4月1日-5月5日在文明古都洛阳举行,某初中学校为了了解本校2500名学生对此次文化节的关注程度,随机抽取了200名学生进行调查,按关注程度绘成了条形统计图(如图).已知一般关注的人数占被调查人数的45%.
第33届“中国洛阳牡丹文化节”于2015年4月1日-5月5日在文明古都洛阳举行,某初中学校为了了解本校2500名学生对此次文化节的关注程度,随机抽取了200名学生进行调查,按关注程度绘成了条形统计图(如图).已知一般关注的人数占被调查人数的45%.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
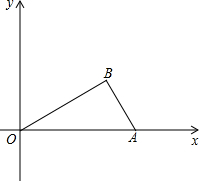 如图,在平面直角坐标系中,Rt△ABO的斜边OA在x轴上,点B在第一象限内,AO=4,∠BOA=30°.点C(t,0)是x轴正半轴上一动点(t>0且t≠4):
如图,在平面直角坐标系中,Rt△ABO的斜边OA在x轴上,点B在第一象限内,AO=4,∠BOA=30°.点C(t,0)是x轴正半轴上一动点(t>0且t≠4):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
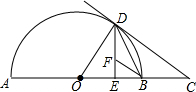 如图,AB是半圆O的直径,过半圆O上一点D作DE⊥AB,垂足为E,作半圆O的切线DC,交AB的延长线于点C,连结OD、BD.
如图,AB是半圆O的直径,过半圆O上一点D作DE⊥AB,垂足为E,作半圆O的切线DC,交AB的延长线于点C,连结OD、BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
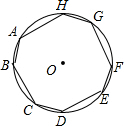 如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )
如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )| A. | 120° | B. | 125° | C. | 130° | D. | 135° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
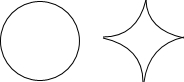 如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )| A. | $\frac{4-π}{π}$ | B. | $\frac{{\sqrt{2}}}{π}$ | C. | $\frac{π-1}{π}$ | D. | $\frac{3}{π}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com