
【题目】随着深圳东进战略的加速实施,市勘探工程队在坪山沿惠州方向一山坡平台处搭建临时工棚.为方便搬运器材,决定降低平台CE前的坡度,已知平台与地面的铅直高为10米,坡面BC的坡度为1∶1,新坡面的坡度为1∶ ![]() .
.
(1)求新坡面的坡角a;
(2)平台CE前的坡度降低后,原坡面底部正前方7米处(PB的长)地面上有一指示牌P是否会覆盖?请说明理由.
【答案】
(1)
解:如图所示,∵新坡面的坡度为1∶ ![]() ,
,
∴tanα=tan∠CAB= ![]() =
= ![]() ,
,
∴∠α=30°.
答:新坡面的坡角a为30°;
(2)
答:指示牌P会覆盖.
理由:过点C作CD⊥AB于点D,则CD=10,
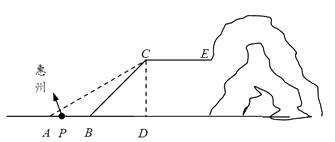
∵坡面BC的坡度为1∶1,新坡面的坡度为1∶ ![]() ,
,
∴BD=CD=10,AD=10 ![]() ,
,
∴AB=AD-BD=10 ![]() -10>7,
-10>7,
∴指示牌P会覆盖.
【解析】(1)由新坡面的坡度为1:![]() , 可得tanα=tan∠CAB=
, 可得tanα=tan∠CAB=![]() =
=![]() , 然后由特殊角的三角函数值,求得答案;
, 然后由特殊角的三角函数值,求得答案;
(2)首先过点C作CD⊥AB于点D,由坡面BC的坡度为1:1,新坡面的坡度为1:![]() , 即可求得AD,BD的长,继而求得AB的长,则可求得答案.
, 即可求得AD,BD的长,继而求得AB的长,则可求得答案.
【考点精析】通过灵活运用关于坡度坡角问题,掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是( )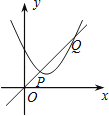
A.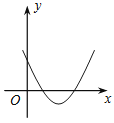
B.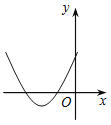
C.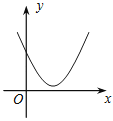
D.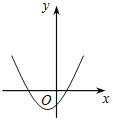
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCO为正方形,A点坐标为(0,2),点P为x轴负半轴上一动点,以AP为直角作等腰直角三角形APD,∠APD=90°(点D落在第四象限)
(1)当点P的坐标为(﹣1,0)时,求点D的坐标;
(2)点P在移动的过程中,点D是否在直线y=x﹣2上?请说明理由;
(3)连接OB交AD于点G,求证:AG=DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,O表示原点,A、B两点分别表示﹣8和2.
(1)求出线段AB的长度;
(2)动点P从A出发沿数轴向右运动,速度为每秒5个单位长度;同时点Q从B出发,沿数轴向右运动,速度为每秒3个单位长度,当P、Q重合时,两点同时停止运动.设两点运动时间为t秒,用含有t的式子表示线段PQ的长;
(3)在(2)的条件下,t为何值时,点P、点Q到原点O的距离相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的顶点B在反比例函数 ![]() 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( )
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( ) 
A.12
B.4 ![]()
C.12-3 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC= ![]() ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为米.
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
数学活动课上,老师出了一道作图问题:“如图,已知直线l和直线l外一点P.用直尺和圆规作直线PQ,使PQ⊥l于点Q.”

小艾的作法如下:
(1)在直线l上任取点A,以A为圆心,AP长为半径画弧.
(2)在直线l上任取点B,以B为圆心,BP长为半径画弧.
(3)两弧分别交于点P和点M
(4)连接PM,与直线l交于点Q,直线PQ即为所求.
老师表扬了小艾的作法是对的.
请回答:小艾这样作图的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“626国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作如表频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:
少分数段(x表示分数) | 频数 | 频率 |
50≤x<60 | 4 | 0.1 |
60≤x<70 | a | 0.2 |
70≤x<80 | 12 | b |
80≤x<90 | 10 | 0.25 |
90≤x<100 | 6 | 0.15 |

(1)表中a= , b= , 并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段80≤x<100对应扇形的圆心角度数是;
(3)请估计该年级分数在60≤x<100的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)连接DE,BF,若BD⊥EF,试探究四边形EBFD的形状,并对结论给予证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com