
����Ŀ���������ϣ�O��ʾԭ�㣬A��B����ֱ��ʾ��8��2��
(1)����߶�AB�ij��ȣ�
(2)����P��A���������������˶����ٶ�Ϊÿ��5����λ���ȣ�ͬʱ��Q��B�����������������˶����ٶ�Ϊÿ��3����λ���ȣ���P��Q�غ�ʱ������ͬʱֹͣ�˶����������˶�ʱ��Ϊt�룬�ú���t��ʽ�ӱ�ʾ�߶�PQ�ij���
(3)��(2)�������£�tΪ��ֵʱ����P����Q��ԭ��O�ľ�����ȣ�

���𰸡�(1)AB��10��(2) PQ��10��2t��0��t��5��(3)Ϊ0.75��5ʱ����P����Q��ԭ��O�ľ�����ȣ�
��������
��1���õ�A��ԭ��O�ľ�����ϵ�B��ԭ��O�ľ��룬��������߶�AB�ij��ȣ�
��2�����߶�AB�ij��ȼ�ȥ����P�����˶��ij��ȣ��ټ��϶���Q�����˶��ij��ȣ��ú���t�Ĵ���ʽ��ʾ�߶�PQ�ij����ɣ�
��3���������⣬������������ٵ�P����Q�غ�ʱ���ڵ�P����Q��ԭ��O������ʱ�����tΪ��ֵʱ����P����Q��ԭ��O�ľ�����ȼ��ɣ�
(1)AB��OA+OB��8+2��10,
(2)PQ��10��5t+3t��10��2t,
��10��2t��0��
���0��t��5��
(3)����P����Q�غ�ʱ��
��10��2t��0��
���t��5��
����P����Q��ԭ��O������ʱ��
OP��8��5t,
OQ��2+3t,
��8��5t��2+3t,
���t��0.75,
����tΪ0.75��5ʱ����P����Q��ԭ��O�ľ�����ȣ�


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ξ������Ʊ�۸����±���
��Ʊ��������λ�ˣ� | 1��50 | 51��100 | 100���� |
ÿ����Ʊ�ۣ���λԪ�� | 80 | 75 | 70 |
ij������ƻ����ס������������Ź�100���˼ƻ�ȥ�����þ��㣬���м���������������50�ˣ���������������50 ���˵�����100�ˣ�����������Ŷ��Ը�������Ϊ��λ������Ʊ����һ��֧��7965Ԫ�����������������������Ϊһ�����幺Ʊ����ֻ�ܻ���7210Ԫ�����������Ÿ��ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3.15��ֲ���ڻ��ijУ�����µļס��ҡ��������ĸ�Ʒ�ֵ�������гɻ��ʹ۲⣬�����Ǹ��ݹ۲������Ƴɵ�ͳ��ͼ����һ���֣� ��1�����µĸ�Ʒ���������ͳ�Ʊ���
ֲ��Ʒ�� | ���� | ���� | ���� | ���� |
ֲ������ | 150 | 125 | 125 |
�������������Ϣ����������⣺
��1��������µ��ĸ�Ʒ�ֵ����繲�ã���Ʒ�������ã�
��2��ͼ1�У���%����%��
��3����֪��������ɻ���Ϊ90%����ͼ2���������� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ϻ�������½���ɫˮ����С���������ȹ�����2ǧ�����Ϻ�3ǧ����ϣ�������9Ԫ�����ֹ�����1ǧ�����Ϻ�2ǧ����ϣ�������5.5Ԫ����ÿ������ˮ�����ۼ۶����䣩
��1��������ˮ�����ۼ۷ֱ���ÿǧ�˶���Ԫ��
��2��������蹺������ˮ����12ǧ�ˣ�Ҫ����ϵ��������������������������������һ�ֹ�����ʹ�����ܷ�����ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABP�У�C��BP����һ�㣬��PAC=��PBA����O�ǡ�ABC�����Բ��AD�ǡ�O��ֱ�����ҽ�BP�ڵ�E�� 
��1����֤��PA�ǡ�O�����ߣ�
��2������C��CF��AD������Ϊ��F���ӳ�CF��AB�ڵ�C����ACAB=12����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O�У�ֱ��CD����AB�������н�������ȷ���ǣ� �� 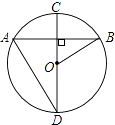
A.AD=AB
B.��BOC=2��D
C.��D+��BOC=90��
D.��D=��B
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ڶ���ս�Եļ���ʵʩ���п�̽���̶���ƺɽ�ػ��ݷ���һɽ��ƽ̨�����ʱ���Ϊ����������ģ���������ƽ̨CEǰ���¶ȣ���֪ƽ̨������Ǧֱ��Ϊ10�ף�����BC���¶�Ϊ1��1����������¶�Ϊ1�� ![]() ��
��
��1������������½�a��
��2��ƽ̨CEǰ���¶Ƚ��ͺ�ԭ����ײ���ǰ��7�״���PB�ij�����������һָʾ��P�Ƿ�Ḳ�ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��չ��������Ƽ����±������,��ϲ�����������������һ��ң�س���ֱ�߹��AC������ֱ���˶���ģ��.�ס�������ͬʱ�ֱ��A,B����,�ع������C��,��AC��,���ٶ����ҵ��ٶȵ�1.5��,��t�ֺ�ס�����ң�س���B���ľ���ֱ�Ϊd1,d2(��λ:��),��d1,d2��t�ĺ�����ϵ��ͼ,�Ը���ͼ������������.

��1��������ҵ��ٶ�v2=________��/��;
��2��д��d1��t�ĺ�������ʽ;
��3�����ס�����ң�س��ľ��볬��10��ʱ�źŲ�����������,��̽��ʲôʱ����ң�س����źŲ�����������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC��AB=AC=5��BC=8����PDQ�Ķ���D��BC���ϣ�DP��AB���ڵ�E��DQ��AB���ڵ�O�ҽ�CA���ӳ����ڵ�F����F���A���غϣ������PDQ=��B��BD=3��
��1����֤����BDE�ס�CFD��
��2����BE=x��OA=y����y����x�ĺ�����ϵʽ����д��������
��3������AOF�ǵ���������ʱ����BE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com