Question

【题目】如图，在⊙O中，直径CD⊥弦AB，则下列结论中正确的是（ ）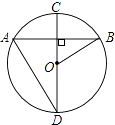
A.AD=AB
B.∠BOC=2∠D
C.∠D+∠BOC=90°
D.∠D=∠B

Answer 1

【答案】B
【解析】解：A、根据垂径定理不能推出AD=AB，故A选项错误； B、∵直径CD⊥弦AB，
∴ = ，
∵ 对的圆周角是∠ADC， 对的圆心角是∠BOC，
∴∠BOC=2∠ADC，故B选项正确；
C、根据已知推出∠BOC=2∠ADC，不能推出3∠ADC=90°，故C选项错误；
D、根据已知不能推出∠DAB=∠BOC，不能推出∠D=∠B，故D选项错误；
故选：B．
【考点精析】利用垂径定理和圆周角定理对题目进行判断即可得到答案，需要熟知垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．