
【题目】用适当的方法解下列方程.
(1)(x﹣3)2=2(x﹣3);
(2)9x2﹣3=22;
(3)x2﹣6x﹣98=0;
(4)3x2﹣1=2x+2;
(5)(3m+2)2﹣7(3m+2)+10=0.
【答案】(1)x=3或x=5;(2)x=±![]() ;(3)x=3±
;(3)x=3±![]() ;(4)x=
;(4)x=![]() ;(5)m=0或m=1
;(5)m=0或m=1
【解析】
(1)利用因式分解法求解可得;
(2)利用直接开平方法求解可得;
(3)利用配方法求解可得;
(4)整理为一般式后利用公式法求解可得;
(5)利用因式分解法求解可得.
解:(1)∵(x﹣3)2﹣2(x﹣3)=0,
∴(x﹣3)(x﹣5)=0,
则x﹣3=0或x﹣5=0,
解得x=3或x=5;
(2)∵9x2=25,
∴x2=![]() ,
,
则x=±![]() ;
;
(3)∵x2﹣6x=98,
∴x2﹣6x+9=98+9,即(x﹣3)2=107,
则x﹣3=±![]() ,
,
∴x=3±![]() ;
;
(4)∵3x2﹣2x﹣3=0,
∴a=3,b=﹣2,c=﹣3,
则△=(﹣2)2﹣4×3×(﹣3)=40>0,
∴x=![]() =
=![]() ;
;
(5)∵(3m+2)2﹣7(3m+2)+10=0,
∴(3m+2﹣2)(3m+2﹣5)=0,
∴3m+2﹣2=0或3m+2﹣5=0,
解得m=0或m=1.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图:反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,其中
两点,其中![]() 点坐标为
点坐标为![]() .
.

(1)求反比例函数与一次函数的表达式;
(2)观察图象,直接写出当![]() 时,自变量
时,自变量![]() 的取值范围;
的取值范围;
(3)一次函数的图象与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数图象上的一个动点,若
是反比例函数图象上的一个动点,若![]() ,求此时
,求此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为12分米,宽为8分米的矩形铁皮制作一个无盖长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
(1)请在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求当长方体底面面积为32平方分米时,裁掉的正方形边长是多少?
(2)若要求制作的长方体的底面长不大于底面宽的5倍(长大于宽),并将容器外表面进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,求裁掉的正方形边长为多少时,总费用最低,最低费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=![]() ,其中正确的有( )
,其中正确的有( )
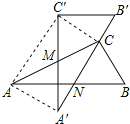
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线x=1为对称轴的抛物线y=-x2+bx+c与x轴交于A、B两点,其中点A的坐标为(3,0).
(1)求点B的坐标;
(2)设点M(x1,y1)、N(x2,y2)在抛物线线上,且x1<x2<1,试比较y1、y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:① PA=PB+PC,② ![]() ;③ PA·PE=PB·PC.其中,正确结论的个数为( )。
;③ PA·PE=PB·PC.其中,正确结论的个数为( )。
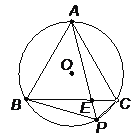
A.3个 B.2个 C.1个 D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 ![]() 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
(1)写出不等式 ![]() 的解集;
的解集;
(2)写出 ![]() 随
随 ![]() 的增大而减小的自变量
的增大而减小的自变量 ![]() 的取值范围;
的取值范围;
(3)分别求出 ![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.
(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=3秒时,P、Q两点之间的距离是多少?
(3)当t为多少秒时,以点C、P、Q为顶点的三角形与△ABC相似?
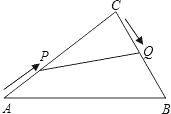
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com