
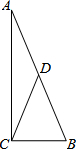
 如图,在△ABC中,∠C=90°,点D为AB的中点,BC=3,AB=9,△DBC沿着CD翻折后,点B落到点E,那么AE的长为7.
如图,在△ABC中,∠C=90°,点D为AB的中点,BC=3,AB=9,△DBC沿着CD翻折后,点B落到点E,那么AE的长为7. 分析 先由勾股定理求得AC的长,然后可求得sin∠DBC的值,然后证明∠DCB=∠DBC,由OB=CBsin∠DCB可求得OB的长,然后可得到BE的长,然后依据三角形的中线的性质可得到AE∥CD,则△AEB为直角三角形,最后依据勾股定理求解即可.
解答 解:如图所示:连接BE.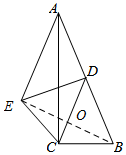
在Rt△ABC中,由勾股定理可知AC=$\sqrt{A{B}^{2}-C{B}^{2}}$=6$\sqrt{2}$.
∴sin∠ABC=$\frac{6\sqrt{2}}{9}$=$\frac{2\sqrt{2}}{3}$.
∵∠ACB=90°,D是AB的中点,
∴DC=BD=AD.
∴∠DCB=∠DBC.
∴BO=BCsin∠DCB=3×$\frac{2\sqrt{2}}{3}$=2$\sqrt{2}$.
由翻折的性质可知BE⊥CD,OE=OB.
∵AD=BD,OB=OE,
∴AE∥OD,BE=4$\sqrt{2}$,
∴∠AEB=90°.
在Rt△ABE中,依据勾股定理可知AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=7.
故答案为:7.
点评 本题主要考查的是翻折的性质、勾股定理、直角三角形斜边上中线的性质,证得△ABE为直角三角形是解题的关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
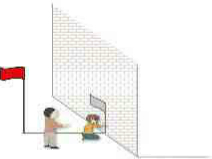 小聪和他的同学利用影长测量旗杆高度(如图),当1m长的直立竹竿的影长为1.5m时,测量旗杆落在地上的影长为21m,落在墙上的影长为2m,求旗杆的高度.
小聪和他的同学利用影长测量旗杆高度(如图),当1m长的直立竹竿的影长为1.5m时,测量旗杆落在地上的影长为21m,落在墙上的影长为2m,求旗杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
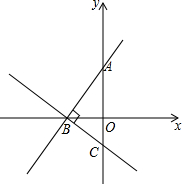 如图,直线y=$\frac{1}{2}$x+2与两坐标轴分别交于A,B两点,直线BC与直线AB垂直,垂足为B,则直线BC所对应的函数解析式为y=-2x-8.
如图,直线y=$\frac{1}{2}$x+2与两坐标轴分别交于A,B两点,直线BC与直线AB垂直,垂足为B,则直线BC所对应的函数解析式为y=-2x-8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
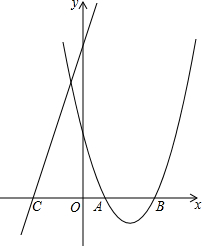 已知抛物线y=x2-(k+2)x+$\frac{5k+2}{4}$和直线y=(k+1)x+(k+1)2
已知抛物线y=x2-(k+2)x+$\frac{5k+2}{4}$和直线y=(k+1)x+(k+1)2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在一幅长80厘米,宽50厘米的矩形风景画的四周镶一条金色的纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400平方厘米,设金色纸边的宽为x厘米,那么满足的方程是( )
在一幅长80厘米,宽50厘米的矩形风景画的四周镶一条金色的纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400平方厘米,设金色纸边的宽为x厘米,那么满足的方程是( )| A. | x2+130x-1400=0 | B. | x2-130x-1400=0 | C. | x2+65x-350=0 | D. | x2-65x-350=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com