
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法: ①c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am2+bm+a>0(m≠﹣1).
其中正确的个数是( )
A.1
B.2
C.3
D.4
【答案】C
【解析】解:抛物线与y轴交于原点, c=0,(故①正确);
该抛物线的对称轴是: ![]() ,
,
直线x=﹣1,(故②正确);
当x=1时,y=a+b+c
∵对称轴是直线x=﹣1,
∴﹣b/2a=﹣1,b=2a,
又∵c=0,
∴y=3a,(故③错误);
x=m对应的函数值为y=am2+bm+c,
x=﹣1对应的函数值为y=a﹣b+c,
又∵x=﹣1时函数取得最小值,
∴a﹣b+c<am2+bm+c,即a﹣b<am2+bm,
∵b=2a,
∴am2+bm+a>0(m≠﹣1).(故④正确).
故选:C.
【考点精析】根据题目的已知条件,利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
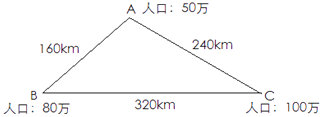
【题目】据有关资料统计,两个城市之间每天的电话通话次数T与这两个城市的人口数xy(单位:万人)以及两城市间的距离l(单位:km)之间有下列关系式![]() (k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)
(k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
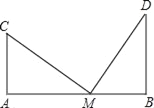
【题目】如图,两根旗杆AC与BD相距12m,某人从B点沿AB走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为0、5m/s,求这个人走了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.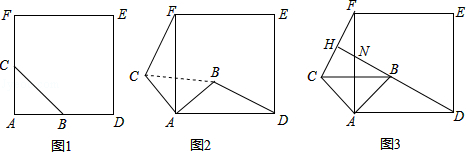
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3 ![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的有( )
①一个三角形至少有2个锐角;②在△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形;③过n边形的一个顶点可作(n﹣3)条对角线;④n边形每增加一条边,则其内角和增加360°.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
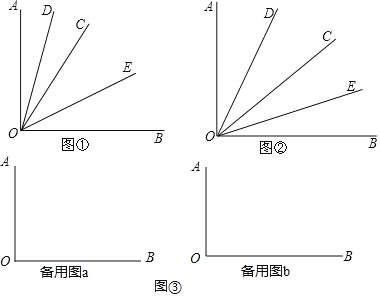
【题目】已知:∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,若射线OC在∠AOB内部绕O点旋转,当∠BOC=α时,求∠DOE的度数.
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)B出发后______小时与A相遇.
(4)若B的自行车不发生故障,保持出发时的速度前进,______小时与A相遇,相遇点离B的出发点______千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:一列数x1,x2,x3,……,xn,从这列数的第二项数起,每一项与它前面的项的比都等于一个常数,就把这样的一列数叫做等比数列,这个常数叫做等比数列的公比.如1,2,4,8,…….这列数就是等比数列,公比是2.
(1)等比数列5,-15,45,-135,……,请计算这个等比数列的公比?
(2)若一个等比数列:-9,a,b,……,的公比是-![]() ,求a,b的值.
,求a,b的值.
(3)一个等比数列的第二项是-10,第三项是-20,求这组数列的第一项和第五项.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元问平均每人捐款是多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com