
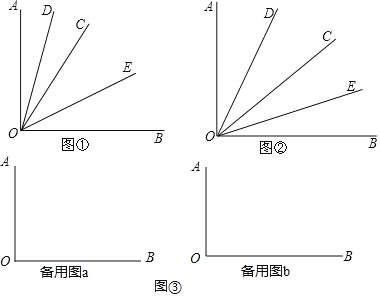
【题目】已知:∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,若射线OC在∠AOB内部绕O点旋转,当∠BOC=α时,求∠DOE的度数.
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,直接写出∠DOE的度数.
【答案】(1)45°;(2)45°;(3)45°或135°.
【解析】
(1)由∠BOC的度数求出∠AOC的度数,利用角平分线定义求出∠COD与∠COE的度数,相加即可求出∠DOE的度数;
(2)∠DOE度数不变,理由为:利用角平分线定义得到∠COD为∠AOC的一半,∠COE为∠COB的一半,而∠DOE=∠COD+∠COE,即可求出∠DOE度数为45度;
(3)分两种情况考虑,同理如图3,则∠DOE为45°;如图4,则∠DOE为135°.
(1)如图,∠AOC=90°﹣∠BOC=20°,

∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOC=10°,∠COE=![]() ∠BOC=35°,
∠BOC=35°,
∴∠DOE=∠COD+∠COE=45°;
(2)∠DOE的大小不变,理由是:
∠DOE=∠COD+∠COE=![]() ∠AOC+
∠AOC+![]() ∠COB=
∠COB=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)=![]() ∠AOB=45°;
∠AOB=45°;
(3)∠DOE的大小发生变化情况为:如图③,则∠DOE为45°;如图④,则∠DOE为135°,
分两种情况:如图3所示,
∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=∠COD﹣∠COE=![]() (∠AOC﹣∠BOC)=45°;
(∠AOC﹣∠BOC)=45°;
如图4所示,∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ×270°=135°.
×270°=135°.


科目:初中数学 来源: 题型:
【题目】小华家买了一辆轿车,他连续10天记录了他家轿车每天行驶的路程,以30千米为标准,超过或不足部分分别用正数、负数表示,得到的数据如下(单位:千米):+3,+1,![]() ,+9,
,+9,![]() ,+2.5,
,+2.5,![]() ,+4.5,
,+4.5,![]() ,+2
,+2
(1)请你运用所学知识估计小华家一个月(按30天算)轿车行驶的路程;
(2)若已知该轿车每行驶100千米耗油8升,目前汽油价格为每升7.8元,试根据(1)题估计小
华家一年(按12个月算)的汽油费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 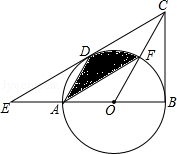
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块长为a米,宽为b米的矩形空地建成一个矩形花园,要求在花园中修两条入口宽均为x米的小道,其中一条小道两边分别经过矩形一组对角顶点,剩余的地方种植花草,现有从左至右三种设计方案如图所示,种植花草的面积分别为S1,S2和S3,则它们的大小关系为( )

A. S3<S1<S2 B. S1<S2<S3 C. S2<S1<S3 D. S1=S2=S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法: ①c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am2+bm+a>0(m≠﹣1).
其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
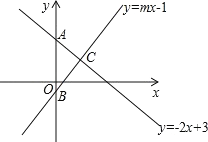
【题目】如图,直线y1=-2x+3和直线y2=mx-3分别交y轴于点A、B ,两直线交于点C(1,n).
(1)求 m、n 的值;
(2)求△ABC的面积;
(3)请根据图象直接写出:当 y1<y2时,自变量 x 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com