
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D落在AB边上,斜边DE交AC于点F,则n的大小和图中阴影部分的面积分别为( )

A. 30,2 B. 60,2 C. 60,![]() D. 60,
D. 60,![]()
【答案】C
【解析】
先根据已知条件求出AC的长及∠B的度数,再根据图形旋转的性质及等边三角形的判定定理判断出△BCD的形状,进而得出∠DCF的度数,由直角三角形的性质可判断出DF是△ABC的中位线,由三角形的面积公式即可得出结论.
解答:解:∵△ABC是直角三角形,∠ACB=90°,∠A=30°,BC=2,
∴∠B=60°,AC=BC×cot∠A=2×![]() =2
=2![]() ,AB=2BC=4,
,AB=2BC=4,
∵△EDC是△ABC旋转而成,
∴BC=CD=BD=![]() AB=2,
AB=2,
∵∠B=60°,
∴△BCD是等边三角形,
∴∠BCD=60°,
∴∠DCF=30°,∠DFC=90°,即DE⊥AC,
∴DE∥BC,
∵BD=![]() AB=2,
AB=2,
∴DF是△ABC的中位线,
∴DF=![]() BC=
BC=![]() ×2=1,CF=
×2=1,CF=![]() AC=
AC=![]() ×2
×2![]() =
=![]() ,
,
∴S阴影=![]() DF×CF=
DF×CF=![]() ×
×![]() =
=![]() .
.
故选C.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C. 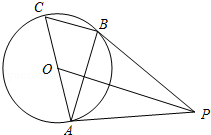
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: ![]() ,
, ![]() ,结果保留整数.)
,结果保留整数.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小冬与小夏是某中学篮球队的队员,在最近五场球赛中的得分如下表所示:
第一场 | 第二场 | 第三场 | 第四场 | 第五场 | |
小冬 |
|
|
|
|
|
小夏 |
|
|
|
|
|
(1)根据上表所给的数据,填写下表:
平均数 | 中位数 | 众数 | 方差 | |
小冬 |
|
|
| |
小夏 |
|
|
|
(2)根据以上信息,若教练选择小冬参加下一场比赛,教练的理由是什么?
(3)若小冬的下一场球赛得分是![]() 分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(
分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 三个顶点的坐标分别为 A(1,1),B(4,2),C(3,4).
(1)请画出△ABC 向左平移 5 个单位长度后得到的△A1B1C1;
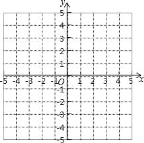
(2)在 x 轴上求作一点 P,使△PAB 的周长最小,请画出△PAB,并直接写出 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是Rt△ABC的外接圆,AC是⊙O的直径,弦BD=BA,AB=12,BC=5,BE⊥DC,交DC的延长线于点E. 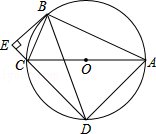
(1)求证:△ABC∽△DEB;
(2)求证:BE是⊙O的切线;
(3)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车沿同一路线从A地前往B地,甲车以a千米时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙车在甲车出发2小时后匀速前往B地,比甲车早30分钟到达.到达B地后,乙车按原速度返回A地,甲车以2a千米时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(小时),s与t之间的函数图象如图所示,求两车在途中第二次相遇时t的值_____.
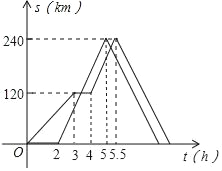
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com