
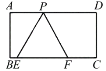
【题目】如图,已知矩形![]() ,在
,在![]() 上取两点
上取两点![]() 在
在![]() 左边),以
左边),以![]() 为边作等边三角形
为边作等边三角形![]() ,使顶点
,使顶点![]() 在
在![]() 上.
上.
(1)求△PEF的边长;
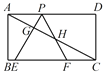
(2)若△PEF的边![]() 在线段
在线段![]() 上移动.
上移动.![]() 分别交
分别交![]() 于点
于点![]() .求证:
.求证:![]() .
.
【答案】(1)![]() 边长为
边长为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)要求△PEF的边长,需构造直角三角形,那么就过P作PQ⊥BC于Q.利用∠PFQ的正弦值可求出PF,即△PEF的边长;
(2)利用∠1的正切值可求出∠1的度数,再由∠PFE=60°,可得出△HFC是等腰三角形,因此就有BE+EF+CF=BE+PH+2FH=3.再把其中FH用PH表示,化简即可.
(1)过P作PQ⊥BC于Q.
∵矩形ABCD中,∠B=90°,即AB⊥BC.
又∵AD∥BC,
∴PQ=AB![]() .
.
∵△PEF是等边三角形,
∴∠PFQ=60°.
在Rt△PQF中,PF![]() 2,
2,
∴△PEF的边长为2;
(2)在Rt△ABC中,AB![]() ,BC=3,
,BC=3,
∴AC![]() ,
,
∴tan∠1=![]() ,
,
∴∠1=30°.
∵△PEF是等边三角形,
∴∠PFE=60°,PF=EF=2.
∵∠PFE=∠1+∠4,
∴∠4=30°,
∴∠1=∠4,
∴FC=FH.
∵PH+FH=2,BE+FC=3﹣EF=3﹣2=1,
∴PH﹣BE=(PH+FH)-(BE+FC)=1.


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长都是1的方格纸中,有线段AC和EF,点A、C、E、F都在小正方形的顶点上.
(1)在方格纸中画出一个以线段AC为对角线的正方形ABCD,所画的正方形的各顶点必须在小正方形的顶点上.
(2)在方格纸中以EF为腰画出等腰三角形△EFM,点M在小正方形的顶点上,且MF=MC.
(3)在(1)、(2)的条件下,连接MA,请直接写出线段MA的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山种了44棵苹果树.现在进入第三年收获期.收获时,先随意摘了5棵树上的苹果,称得每棵树摘得的苹果重量如下(单位:千克)35 35 34 39 37
(1)在这个问题中,总体指的是?个体指的是?样本是?样本容量是?
(2)试根据样本平均数去估计总体情况,你认为该农户可收获苹果大约多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
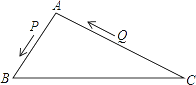
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:①△BMD≌△DFE;②△NBE∽△DBC;③AC=2DF;④EFAB=CFBC,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
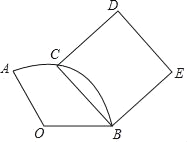
【题目】如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在![]() 上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是_____.
上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+ c(a≠0).
(1)若抛物线与x轴交于点B(4,0),且过点P(1,–3),求该抛物线的解析式;
(2)若a>0,c =0,OA、OB是过抛物线顶点的两条互相垂直的直线,与抛物线分别交于A、B 两点,求证:直线AB恒经过定点(0,![]() );
);
(3)若a>0,c <0,抛物线与x轴交于A,B两点(A在B左边),顶点为C,点P在抛物线上且位于第四象限.直线PA、PB与y轴分别交于M、N两点.当点P运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com