练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知△ABC中，∠A＝25°，∠B＝40°．

    （1）求作：⊙O，使⊙O经过A、C两点，且圆心落在AB边上；

    （要求：尺规作图，保留作图痕迹，不写作法．）

    （2）求证：BC是（1）中所作⊙O的切线．

    【答案】(1)作图见解析；（2）证明见解析.

    【解析】试题分析：（1）作出线段AC的垂直平分线进而得出AC垂直平分线与线段AB的交点O，进而以AO为半径做圆即可.

    （2）连接CO，由圆周角定理和三角形内角和定理，利用已知得出∠OCB=90°，进而求出即可．

    试题解析：解：（1）作图如答图1：

    （2）证明：如答图2，连接OC，

    ∵OA=OC，∠A=25°，∴∠BOC=50°.

    又∵∠B=40，∴∠BOC+∠B=90°.

    ∴∠OCB=90°.

    ∴OC⊥BC.

    ∴BC是⊙O的切线．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．

    原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF＝45°，连接EF，则EF＝BE＋DF，试说明理由．

    （1）思路梳理

    ∵AB＝CD，

    ∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．

    ∵∠ADC＝∠B＝90°，

    ∴∠FDG＝180°，点F、D、G共线．

    根据___________，SAS

    易证△AFG≌___________△AEF

    ，得EF＝BE＋DF．

    （2）类比引申

    如图2，四边形ABCD中，AB＝AD，∠BAD＝90°．点E、F分别在边BC、CD上，∠EAF＝45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系______________∠B+∠D=180°

    时，仍有EF＝BE＋DF．

    （3）联想拓展

    如图3，在△ABC中，∠BAC＝90°，AB＝AC，点D、E均在边BC上，且∠DAE＝45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某小区便民超市为了了解顾客的消费情况，在该小区居民中进行调查，询问每户人家每周到超市的次数，下图是根据调查结果绘制的，请问：

    （1）这种统计图通常被称为什么统计图？（2）此次调查共询问了多少户人家？

    （3）超过半数的居民每周去多少次超市？（4）请将这幅图改为扇形统计图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线AB与函数y＝（x＞0）的图象交于点A（m，2），B（2，n）．过点A作AC平行于x轴交y轴于点C，在y轴负半轴上取一点D，使OD＝OC，且△ACD的面积是6，连接BC．

    （1）求m，k，n的值；

    （2）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图， 在△ABC中，E是BC边上一点，沿AE折叠，点B恰好落在AC边上的点D处，若∠BAC=60°，BE=CD，则∠AED=______ 度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为8，在各边上顺次截取AE=BF=CG=DH=5，则四边形EFGH的面积是（　　）

    A. 30 B. 34 C. 36 D. 40

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在宽20米，长32米的矩形耕地上，修筑同样宽的三条路(两条纵向，一条横向，并且横向与纵向互相垂直)，把这块耕地分成大小相等的六块试验田，要使试验田的面积是570平方米，问道路应该多宽?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

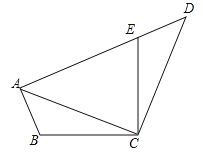
    【题目】如图，已知在四边形ABCD中，点E在AD上，∠BCE=∠ACD=90°，∠BAC=∠D，BC=CE．

    （1）求证：AC=CD；

    （2）若AC=AE，求∠DEC的度数．

    【答案】（1）证明见解析；（2）112.5°．

    【解析】试题分析： 根据同角的余角相等可得到结合条件，再加上 可证得结论；
    根据 得到 根据等腰三角形的性质得到 由平角的定义得到

    试题解析： 证明：

    在△ABC和△DEC中， ，

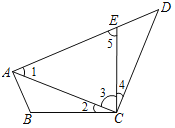
    （2）∵∠ACD＝90°，AC＝CD，

    ∴∠1＝∠D＝45°，

    ∵AE＝AC，

    ∴∠3＝∠5＝67.5°，

    ∴∠DEC＝180°－∠5＝112.5°．

    【题型】解答题
    【结束】
    21

    【题目】一个零件的形状如图所示，工人师傅按规定做得∠B=90°，

    AB＝3，BC＝4，CD＝12，AD＝13，假如这是一块钢板，你能帮工人师傅计算一下这块钢板的面积吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一个底面直径为10cm，高为18cm的圆柱形瓶内装满水，将瓶内的水倒入一个底面直径是12cm，高10cm的圆柱形玻璃杯内，能否完全装下？若装不下，则瓶内水面还有多高？若没装满，求杯内水面的高度．

    查看答案和解析>>

    同步练习册答案