
分析 (1)观察找出规律:左侧分子为1,分母是连续自然数的积,右侧被减数和减数的分子均为1,分母恰为左侧的两个自然数,由此可以写出结果;
(2)根据(1)的规律,将算式写出差的形式,计算即可;
(3)先探索当分母为连续偶数时如何写成差的形式,再计算.
解答 解:(1)观察找出规律:左侧分子为1,分母是连续自然数的积,右侧被减数和减数的分子均为1,分母恰为左侧的两个自然数,
所以:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
故答案为:$\frac{1}{n}$-$\frac{1}{n+1}$.
(2):$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$;
故答案为:$\frac{n}{n+1}$.
(3)$\frac{1}{2×4}$=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$),$\frac{1}{4×6}$=$\frac{1}{2}$($\frac{1}{4}$-$\frac{1}{6}$),$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$)
所以:$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2016×2018}$=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$)+$\frac{1}{2}$($\frac{1}{4}$-$\frac{1}{6}$)+…+$\frac{1}{2}$($\frac{1}{2016}$-$\frac{1}{2018}$)=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{n}$-$\frac{1}{n+2}$)=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{2018}$)=$\frac{252}{1009}$.
点评 此题主要考查有理数的运算和规律研究,分析已知找出运算规律并准确计算是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 3×105 | B. | 3×106 | C. | 3×104 | D. | 30×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
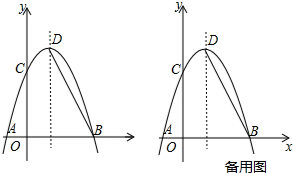
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
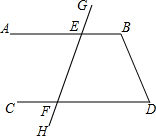 请补全证明过程.如图,已知线段AB,CD与GH相交于点E,F,∠GEB=?,∠EFD=β,∠D=50°,求∠B的度数.
请补全证明过程.如图,已知线段AB,CD与GH相交于点E,F,∠GEB=?,∠EFD=β,∠D=50°,求∠B的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点M是线段AB上 | B. | 点M在直线AB上 | ||
| C. | 点M在直线AB外 | D. | 点M在直线AB上,也可能在直线AB外 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com