
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点. 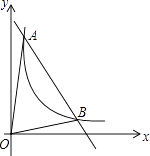
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b< ![]() 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
【答案】
(1)解:∵点A(m,6),B(3,n)两点在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴m=1,n=2,
即A(1,6),B(3,2).
又∵点A(m,6),B(3,n)两点在一次函数y=kx+b的图象上,
∴ ![]() .
.
解得 ![]() ,
,
则该一次函数的解析式为:y=﹣2x+8
(2)解:根据图象可知使kx+b< ![]() 成立的x的取值范围是0<x<1或x>3
成立的x的取值范围是0<x<1或x>3
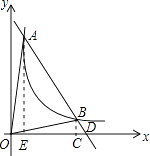
(3)解:分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点.
令﹣2x+8=0,得x=4,即D(4,0).
∵A(1,6),B(3,2),
∴AE=6,BC=2,
∴S△AOB=S△AOD﹣S△BOD= ![]() ×4×6﹣
×4×6﹣ ![]() ×4×2=8.
×4×2=8.
【解析】(1)先把A、B点坐标代入y= ![]() 求出m、n的值;然后将其分别代入一次函数解析式,列出关于系数k、b的方程组,通过解方程组求得它们的值即可;(2)根据图象可以直接写出答案;(3)分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点.S△AOB=S△AOD﹣S△BOD , 由三角形的面积公式可以直接求得结果.
求出m、n的值;然后将其分别代入一次函数解析式,列出关于系数k、b的方程组,通过解方程组求得它们的值即可;(2)根据图象可以直接写出答案;(3)分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点.S△AOB=S△AOD﹣S△BOD , 由三角形的面积公式可以直接求得结果.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】下面是按规律排列的一列数:
第1个式子:1-![]() ;
;
第2个式子:2-![]() ×
×![]() ×
×![]() ;
;
第3个式子:3-![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() .
.
(1)分别计算这三个式子的结果(直接写答案);
(2)写出第2018个式子的形式(中间部分用省略号,两端部分必须写详细),然后计算出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两个点A、B所对应的数为a、b,且a、b满足![]() .
.
(1)求AB的长;

(2)若甲、乙分别从A、B两点同时在数轴上相向运动,甲的速度是2个单位/秒,乙的速度比甲的速度快3个单位/秒,求甲乙相遇点所表示的数;

(3)若点C对应的数为—1,在数轴上A点的左侧是否存在一点P,使PA+PB=3PC?若存在,求出点P所对应的数;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并回答问题:
三峡之最
三峡工程是中国,也是世界上最大的水利枢纽工程,是治理和开发长江的关键性骨干工程.它具有防洪、发电、航运等综合效益.
三峡水库总库容![]() 亿立方米,防洪库容
亿立方米,防洪库容![]() 亿立方米,水库调洪可消减洪峰流量达每秒
亿立方米,水库调洪可消减洪峰流量达每秒![]() ─
─![]() 万立方米,是世界上防洪效益最为显著的水利工程.
万立方米,是世界上防洪效益最为显著的水利工程.
三峡水电站总装机![]() 万千瓦,年发电量
万千瓦,年发电量![]() 亿千瓦.时,是世界上最大的电站.
亿千瓦.时,是世界上最大的电站.
三峡水库回水可改善川江![]() 公里的航道,使宜渝船队吨位由现在的
公里的航道,使宜渝船队吨位由现在的![]() 吨级堤高到万吨级,年单向通过能力由
吨级堤高到万吨级,年单向通过能力由![]() 万吨增加到
万吨增加到![]() 万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.
万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.
思考:
![]() 三峡水电站年发电量
三峡水电站年发电量![]() 亿千瓦.时,一个普通家庭一天用电
亿千瓦.时,一个普通家庭一天用电![]() 千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留
千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留![]() 个有效数字)
个有效数字)
![]() 宜都市
宜都市![]() 万人,平均一户
万人,平均一户![]() 个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数).
个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(![]() +
+![]()
![]() )×(-60) (2) (-
)×(-60) (2) (-![]() )×(-3
)×(-3![]() )÷(-1
)÷(-1![]() )÷3;
)÷3;
(3) (-5)×(-3![]() )+(-7)×(-3
)+(-7)×(-3![]() )+12×(-3
)+12×(-3![]() ) (4) 19
) (4) 19![]() ×(-8)
×(-8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,∠A=36°,AC的垂直平分线MN交AB于D,AC于M,以下结论:
①△BCD是等腰三角形;②射线CD是∠ACB的角平分线;③△BCD的周长C△BCD=AB+BC;④△ADM≌△BCD。
正确的有( )

A. ①② B. ①③ C. ①②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC= ![]() .求证:
.求证: 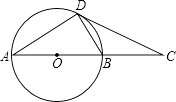
(1)△CDB∽△CAD;
(2)CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:

(1)此次抽查的学生数为 人,并补全条形统计图;
(2)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是 ;
(3)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有 人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com