
【题目】已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC= ![]() .求证:
.求证: 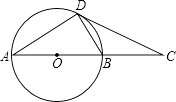
(1)△CDB∽△CAD;
(2)CD是⊙O的切线.
【答案】
(1)证明:∵AB=6,BC=AB,DC= ![]() ,
,
∴AC=12,BC=6.
∴ ![]() .
.
∵∠C=∠C,
∴△CDB∽△CAD
(2)证明:(证法一):连接OD,则有OD=3,
∵OC=9,DC= ![]() ,
,
∵DC2+OD2=(6 ![]() )2+32=81=92
)2+32=81=92
∴DC2+OD2=OC2
∴∠ODC=90°,
∴CD⊥OD.
又∵OD是半径,
∴CD是⊙O的切线.
(证法二):连接OD,则有OD=OA,
∴∠A=∠ADO.
∵△CDB∽△CAD,
∴∠CDB=∠A.
∴∠CDB=∠ADO.
∵AB是⊙O的直径,
∴∠ADB=90°.
即∠ADO+∠ODB=90°.
∴∠CDB+∠ODB=90°.
即∠ODC=90°.
∴CD⊥OD.
∵OD是半径,
∴CD是⊙O的切线.
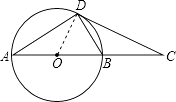
【解析】(1)根据已知及相似三角形的判定方法进行分析即可;(2)连接OD,求出OD2+CD2=OC2 , 根据勾股定理的逆定理得出∠ODC=90°,得出结论.
【考点精析】本题主要考查了切线的判定定理和相似三角形的判定的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,E,F分别在AB,CD上,且BE=DF,EF与BD相交于点O,连结AO.若∠CBD=35°,则∠DAO的度数为( )
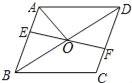
A. 35° B. 55° C. 65° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点. 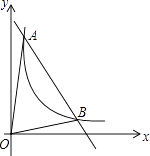
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b< ![]() 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B是数轴上的点,且点A表示数-3,请参照图并思考,完成下列各题:
![]()
(1)将A点向右移动4个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是 .
(2)若把数轴绕点A对折,则对折后,点B落在数轴上的位置所表示的数为 .
(3)若(1)中点B以每秒2个单位长度沿数轴向左运动,A不动,多长时间后,点B与点A距离为2个单位长度?试列式计算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若![]() ,AB=2,则图中阴影部分的面积为( )
,AB=2,则图中阴影部分的面积为( )
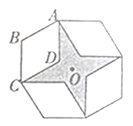
A. 12-4![]() B. 5 C. 12-4
B. 5 C. 12-4![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
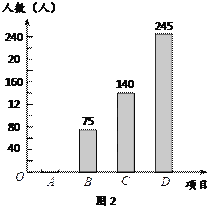
【题目】某校在大课间中开设了A(体操),B(跑操),C(舞蹈),D(健美操)四项活动,为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:
⑴ 这次被调查的学生共有 人.
⑵ 请将统计图2补充完整.
⑶ 已知该校共有学生3400人,请根据调查结果估计该校喜欢健美操的学生人数.
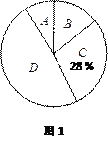
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=ADAC;③ADBC=ABBD;④ABBC=ACBD.其中单独能够判定△ABC∽△ADB的个数是( ) 
A.①②
B.①②③
C.①②④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com