
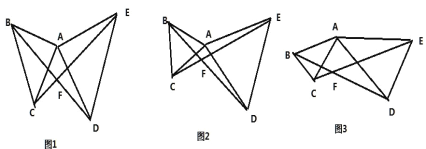
【题目】(1)如图 1,△ABC 和△ADE 都是等腰直角三角形,∠BAC 和∠DAE 是直角,连接BD,CE 相交于点 F,则∠BFC= °
(2)如图 2,△ABC 和△ADE 都是等边三角形,连接 BD,CE 相交于点 F,则∠BFC= °
(3)如图 3,△ABC 和△ADE 都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,连接 BD,CE相交于点 F,请猜想∠BFC 与∠BAC 有怎样的大小关系?请证明你的猜想
【答案】(1)90°;(2)60°;(3)![]() 证明见解析;
证明见解析;
【解析】
(1)求出![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(2)求出![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(3)根据![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(1)如图:
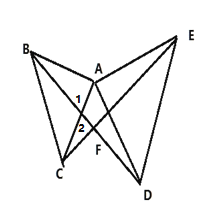
∵△ABC和△ADE都是等腰直角三角形
∴AD=AE,AB=AC,![]()
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
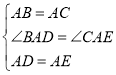 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
故答案为:90°
(2)如图:
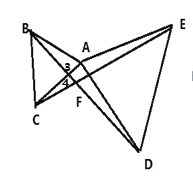
∵△ABC和△ADE都是等边三角形
∴AD=AE,AB=AC,![]()
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
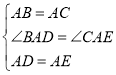 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
故答案为:60°
(3) ![]() 理由如下:
理由如下:
∵∠BAC=∠DAE
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
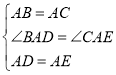 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是二次函数![]() 的图象,其顶点坐标为
的图象,其顶点坐标为![]() .
.

![]() 求出图象与
求出图象与![]() 轴的交点
轴的交点![]() ,
,![]() 的坐标;
的坐标;
![]() 在二次函数的图象上是否存在点
在二次函数的图象上是否存在点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标;若不存在,请说明理由;
点的坐标;若不存在,请说明理由;
![]() 将二次函数的图象在
将二次函数的图象在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线![]() 与此图象有两个公共点时,
与此图象有两个公共点时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
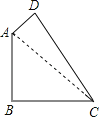
【题目】如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且∠ABC=90°,连接AC.
(1)求AC的长度.
(2)求证△ACD是直角三角形.
(3)求四边形ABCD的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是李刚同学在一次测验中解答的数学题:
①若![]() ,则
,则![]() ,
,
②方程![]() 的解为
的解为![]() ,
,
③若![]() 两根的倒数和等于
两根的倒数和等于![]() ,则
,则![]() ,
,
④若![]() 是方程
是方程![]() 的解,则
的解,则![]() 或
或![]() .
.
其中答对的是________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
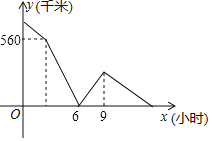
【题目】A、B、C三地在同一直线上,甲、乙两车分别从A,B两地相向匀速行驶,甲车先出发2小时,甲车到达B地后立即调头,并将速度提高10%后与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶,经过一段时间后两车同时到达C地,设两车之间的距离为y(千米),甲行驶的时间x(小时).y与x的关系如图所示,则B、C两地相距_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(c+a)x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状并说明理由;
(2)已知a:b:c=3:4:5,求该一元二次方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=x2-2x-3与x轴相交于点A,B(点A在B的左侧),与y轴相交于点C,直线y2=kx+b经过点B,C.

(1)求直线BC的函数关系式;
(2)当y1>y2时,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中![]() ,
,![]() ,詹姆斯在探究筝形的性质时,得到如下结论:
,詹姆斯在探究筝形的性质时,得到如下结论:![]() ;
;![]() ;
;![]() ≌
≌![]() ;
;![]() 四边形ABCD的面积
四边形ABCD的面积![]() 其中正确的结论有
其中正确的结论有![]()
![]()

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com