
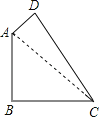
【题目】如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且∠ABC=90°,连接AC.
(1)求AC的长度.
(2)求证△ACD是直角三角形.
(3)求四边形ABCD的面积?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图是一支蜡烛点燃以后,其长度![]() 与时间
与时间![]() 的函数图象,请解答以下问题:
的函数图象,请解答以下问题:

(1)这支蜡烛点燃前的长度是多少cm?每小时燃烧是多少cm?
(2)写出![]() 与
与![]() 的函数解析式,并求
的函数解析式,并求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 某种三角形台历被放置在水平桌面上,其左视图如图
某种三角形台历被放置在水平桌面上,其左视图如图![]() ,其中点
,其中点![]() 是台历支架
是台历支架![]() 、
、![]() 的交点,同时又是台历顶端连接日历的螺旋线圈所在圆的圆心.现测得
的交点,同时又是台历顶端连接日历的螺旋线圈所在圆的圆心.现测得![]() ,
,![]() ,
,![]() .
.
![]() 求点
求点![]() 到直线
到直线![]() 的距离;
的距离;
![]() 求张角
求张角![]() 的大小;
的大小;
![]() 现把某月的日历从台历支架正面翻到背面(即
现把某月的日历从台历支架正面翻到背面(即![]() 与
与![]() 重合),求点
重合),求点![]() 所经历的路径长.
所经历的路径长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 取
取![]() ,所有结果精确到
,所有结果精确到![]() ,可使用科学计算器)
,可使用科学计算器)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 、
、![]() ,点
,点![]() 坐标为
坐标为![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 抛物线的顶点为
抛物线的顶点为![]() ,在
,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 最小,并求出点
最小,并求出点![]() 的坐标;
的坐标;
![]() 点
点![]() 是线段
是线段![]() 上的动点,过点
上的动点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .当
.当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 若平行于
若平行于![]() 轴的动直线
轴的动直线![]() 与该抛物线交于点
与该抛物线交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() .问:是否存在这样的直线
.问:是否存在这样的直线![]() ,使得
,使得![]() 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进的乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,购进这两种玩具的总资金超过960元但不超过1000元,求商场有哪几种具体的进货方案?最多可以购进乙种玩具多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+
x+![]() 与y=x相交于点A,与x轴交于点B.
与y=x相交于点A,与x轴交于点B.
(1)填空:A的坐标是_______,B的坐标是___________;
(2)直线y=﹣![]() x+
x+![]() 上有点P(m,n),且点P在第四象限,设△AOP的面积为S,请求出S与m的函数关系式;
上有点P(m,n),且点P在第四象限,设△AOP的面积为S,请求出S与m的函数关系式;
(3)在直线OA上,是否存在一点D,使得△DOB是等腰三角形?如果存在,试求出所有符合条件的点D的坐标,如果不存在,请说明理由.
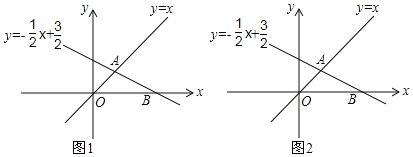
查看答案和解析>>
科目:初中数学 来源: 题型:
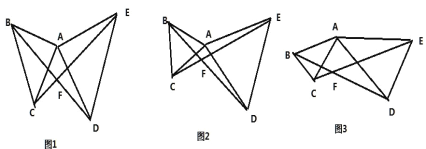
【题目】(1)如图 1,△ABC 和△ADE 都是等腰直角三角形,∠BAC 和∠DAE 是直角,连接BD,CE 相交于点 F,则∠BFC= °
(2)如图 2,△ABC 和△ADE 都是等边三角形,连接 BD,CE 相交于点 F,则∠BFC= °
(3)如图 3,△ABC 和△ADE 都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,连接 BD,CE相交于点 F,请猜想∠BFC 与∠BAC 有怎样的大小关系?请证明你的猜想
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 分别是线段
分别是线段![]() ,
,![]() 上的点,连接
上的点,连接![]() ,使四边形
,使四边形![]() 为正方形,若点
为正方形,若点![]() 是
是![]() 上的动点,连接
上的动点,连接![]() ,将矩形沿
,将矩形沿![]() 折叠使得点
折叠使得点![]() 落在正方形
落在正方形![]() 的对角线所在的直线上,对应点为
的对角线所在的直线上,对应点为![]() ,则线段
,则线段![]() 的长为________.
的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
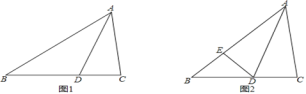
【题目】在△ABC中,AD是它的角平分线.
(1)如图1,求证:S△ABD:S△ACD=AB:AC=BD:CD;
(2)如图2,E是AB上的点,连接ED,若BD=3,BE=CD=2,AE=2CD,求证:△BED是等腰三角形;
(3)在图1中,若3∠BAC=2∠C,∠ADB>∠B>∠BAD,直接写出∠BAC的取值范围 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com