
【题目】如图![]() 某种三角形台历被放置在水平桌面上,其左视图如图
某种三角形台历被放置在水平桌面上,其左视图如图![]() ,其中点
,其中点![]() 是台历支架
是台历支架![]() 、
、![]() 的交点,同时又是台历顶端连接日历的螺旋线圈所在圆的圆心.现测得
的交点,同时又是台历顶端连接日历的螺旋线圈所在圆的圆心.现测得![]() ,
,![]() ,
,![]() .
.
![]() 求点
求点![]() 到直线
到直线![]() 的距离;
的距离;
![]() 求张角
求张角![]() 的大小;
的大小;
![]() 现把某月的日历从台历支架正面翻到背面(即
现把某月的日历从台历支架正面翻到背面(即![]() 与
与![]() 重合),求点
重合),求点![]() 所经历的路径长.
所经历的路径长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 取
取![]() ,所有结果精确到
,所有结果精确到![]() ,可使用科学计算器)
,可使用科学计算器)

科目:初中数学 来源: 题型:
【题目】某工厂安排甲、乙两个运输队各从仓库调运物资300吨,两队同时开始工作,甲运输队工作3天后因故停止,2天后重新开始工作,由于工厂调离了部分工人,甲运输的工作效率降低到原来的![]() 甲、乙运输队调运物资的数量
甲、乙运输队调运物资的数量![]() 吨
吨![]() 与甲工作时间
与甲工作时间![]() 天
天![]() 的函数图象如图所示.
的函数图象如图所示.
![]() ______;
______;![]() ______.
______.
![]() 求甲运输队重新开始工作后,甲运输队调运物资的数量
求甲运输队重新开始工作后,甲运输队调运物资的数量![]() 吨
吨![]() 与工作时间
与工作时间![]() 天
天![]() 的函数关系式;
的函数关系式;
![]() 直接写出乙运输队比甲运输队多运50吨物资时x的值.
直接写出乙运输队比甲运输队多运50吨物资时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC中,D为AC上一点,E为AB延长线上一点,DE⊥AC交BC于点F,且DF=EF.
(1)求证:CD=BE;
(2)若AB=12,试求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于二次三项式a2+2ab+b2,能直接用完全平方公式进行因式分解,得到结果为(a+b)2.而对于二次三项式a2+4ab﹣5b2,就不能直接用完全平方公式了,但我们可采用下述方法:
a2+4ab﹣5b2=a2+4ab+4b2﹣4b2﹣5b2=(a+2b)2﹣9b2,
=(a+2b﹣3b)(a+2b+3b)=(a﹣b)(a+5b).
像这样把二次三项式分解因式的方法叫做添(拆)项法.
解决问趣:
(1)请利用上述方法将二次三项式a2+6ab+8b2分解因式;
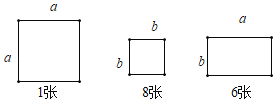
(2)如图,边长为a的正方形纸片1张,边长为b的正方形纸片8张,长为a,宽为b的长方形纸片6张,这些纸片可以拼成一个不重叠,无空隙的长方形图案,请画出示意图;
(3)已知x>0,且x≠2,试比较分式![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是二次函数![]() 的图象,其顶点坐标为
的图象,其顶点坐标为![]() .
.

![]() 求出图象与
求出图象与![]() 轴的交点
轴的交点![]() ,
,![]() 的坐标;
的坐标;
![]() 在二次函数的图象上是否存在点
在二次函数的图象上是否存在点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标;若不存在,请说明理由;
点的坐标;若不存在,请说明理由;
![]() 将二次函数的图象在
将二次函数的图象在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线![]() 与此图象有两个公共点时,
与此图象有两个公共点时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
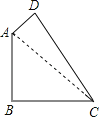
【题目】如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且∠ABC=90°,连接AC.
(1)求AC的长度.
(2)求证△ACD是直角三角形.
(3)求四边形ABCD的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=x2-2x-3与x轴相交于点A,B(点A在B的左侧),与y轴相交于点C,直线y2=kx+b经过点B,C.

(1)求直线BC的函数关系式;
(2)当y1>y2时,请直接写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com