
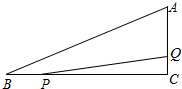
 如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动,动点Q从点C开始沿C-A-B向点B以每秒1个单位长度的速度运动,连接PQ,点P、Q分别从点B、C同时出发,当P点到达C点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动,动点Q从点C开始沿C-A-B向点B以每秒1个单位长度的速度运动,连接PQ,点P、Q分别从点B、C同时出发,当P点到达C点时,另一点也随之停止运动,设运动时间为t秒(t≥0).分析 (1)当CP:BC=CQ:AC时,PQ∥AB,则有(12-2t):12=t:5,即可求出t的值;
(2)以点B为坐标原点,建立平面直角坐标系,由题意可知,当t=5时,点P运动到点D(10,0),DB=10,点Q运动到A点,BC的中点为M(6,0),AD的中点为N;当t=6时,点P运动到C点,点Q运动到K点,AK=1,CK的中点为F,此时P、Q均停止运动,则线段PQ的中点所经过的路程长为线段MN、NF的长度和,利用点M、N的坐标求出MN的长,利用△AKG∽△ABC求出AG、KG的长,进而得出点K、F的坐标,即可求出NF的长.
解答 解:(1)由题意知BP=2t,CP=12-2t,CQ=t,
当CP:BC=CQ:AC时,PQ∥AB,则有(12-2t):12=t:5,
解得:t=$\frac{30}{11}$;
(2)如图,以点B为坐标原点,建立平面直角坐标系,点C的坐标为(12,0),点A的坐标为(12,5),
由题意可知,当t=5时,点P运动到点D(10,0),DB=10,点Q运动到A点,BC的中点为M(6,0),AD的中点为N;当t=6时,点P运动到C点,点Q运动到K点,AK=1,CK的中点为F,此时P、Q均停止运动,则线段PQ的中点所经过的路程长为线段MN、NF的长度和.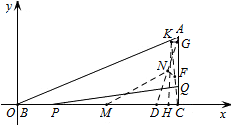
过K作KG⊥AC于G,KH⊥BC于H,
∵D(10,0),A(12,5),N为AD的中点,
∴N(11,$\frac{5}{2}$),
又∵M(6,0),
∴MN=$\sqrt{(6-11)^{2}+(0-\frac{5}{2})^{2}}=\frac{5}{2}\sqrt{5}$;
∵AC=5,BC=12,
∴AB=13,
∵KG⊥AC,∠ACB=90°,
∴KG∥BC,
∴△AKG∽△ABC,
∴AK:AB=AG:AC=KG:BC,即1:13=AG:5=KG:12,
∴AG=$\frac{5}{13}$,KG=$\frac{12}{13}$,
∴CG=AC-AG=$\frac{60}{13}$,BH=BC-KG=$\frac{144}{13}$,
∴K$(\frac{144}{13},\frac{60}{13})$,
又∵C(12,0),F为KC的中点,
∴F$(\frac{150}{13},\frac{30}{13})$,
又∵N(11,$\frac{5}{2}$),
∴NF=$\sqrt{(11-\frac{150}{13})^{2}+(\frac{5}{2}-\frac{30}{13})^{2}}$=$\frac{\sqrt{221}}{26}$,
∴线段PQ的中点所经过的路程长为MN+NF=$\frac{5}{2}\sqrt{5}+\frac{\sqrt{221}}{26}$.
故答案为:(1)$\frac{30}{11}$; (2)$\frac{5}{2}$$\sqrt{5}$+$\frac{\sqrt{221}}{26}$.
点评 本题考查了相似三角形的判定与性质,点的轨迹问题,勾股定理的应用,坐标与图形性质,两点间的距离等知识,正确理解题意,准确画出图形是解题的关键,解题中注意数形结合思想的运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | a<b<d<c | B. | a<d<c<b | C. | b<a<c<d | D. | c<a<d<b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
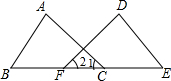 在数学实践课上,老师在黑板上画出如图的图形,(其中点B,F,C,E在同一条直线上).并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
在数学实践课上,老师在黑板上画出如图的图形,(其中点B,F,C,E在同一条直线上).并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
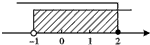 如图,下列哪个不等式组的解集在数轴上表示如图所示( )
如图,下列哪个不等式组的解集在数轴上表示如图所示( )| A. | $\left\{\begin{array}{l}{x≤2}\\{x>-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≥2}\\{x<-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>2}\\{x≤-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<2}\\{x≥-1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
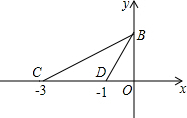 如图,在平面直角坐标系中,C(-3,0),D(-1,0),点B在y轴正半轴上,且tan∠BCO=$\frac{\sqrt{3}}{3}$
如图,在平面直角坐标系中,C(-3,0),D(-1,0),点B在y轴正半轴上,且tan∠BCO=$\frac{\sqrt{3}}{3}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
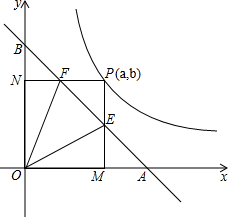 如图,直线与x轴、y轴交于A、B两点,且OA=OB=1,点P是反比例函数$y=\frac{1}{2x}$图象在第一象限的分支上的任意一点,P点坐标为(a,b),由点P分别向x轴,y轴作垂线PM、PN,垂足分别为M、N;PM、PN分别与直线交于点E,点F.
如图,直线与x轴、y轴交于A、B两点,且OA=OB=1,点P是反比例函数$y=\frac{1}{2x}$图象在第一象限的分支上的任意一点,P点坐标为(a,b),由点P分别向x轴,y轴作垂线PM、PN,垂足分别为M、N;PM、PN分别与直线交于点E,点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com