
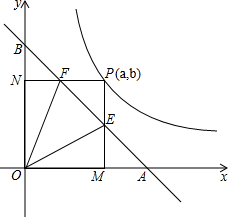
 ��ͼ��ֱ����x�ᡢy�ύ��A��B���㣬��OA=OB=1����P�Ƿ���������$y=\frac{1}{2x}$ͼ���ڵ�һ���ķ�֧�ϵ�����һ�㣬P������Ϊ��a��b�����ɵ�P�ֱ���x�ᣬy��������PM��PN������ֱ�ΪM��N��PM��PN�ֱ���ֱ�߽��ڵ�E����F��
��ͼ��ֱ����x�ᡢy�ύ��A��B���㣬��OA=OB=1����P�Ƿ���������$y=\frac{1}{2x}$ͼ���ڵ�һ���ķ�֧�ϵ�����һ�㣬P������Ϊ��a��b�����ɵ�P�ֱ���x�ᣬy��������PM��PN������ֱ�ΪM��N��PM��PN�ֱ���ֱ�߽��ڵ�E����F������ ��1��������ֱ��EF����ʽΪy=kx+b������֪A��1��0����B��0��1����Ȼ�����ô���ϵ�������ֱ��EF�Ľ���ʽ�����ɵ�P�Ƿ���������$y=\frac{1}{2x}$ͼ���ϣ��ɵ�$b=\frac{1}{2a}$���̶���ô𰸣�
��2����OA=OB=1���ɵ�AB=$\sqrt{2}$����OBA=��OAB=45�㣬�̶���ʾ��BE��AF������֤��BE•AF=OA•OB=1����ɵ�$\frac{BE}{OB}=\frac{OA}{AF}$����OBA=��OAB=45�㣬֤�á�AOF�ס�BEO��
��3���ɡ�AOF�ס�BEO���������������εĶ�Ӧ����ȣ�֤�á�FOA=��OEB����ɵá�FOE=��EAO=45�㣮
��� �⣺��1����ֱ��EF����ʽΪy=kx+b��
����֪A��1��0����B��0��1����
��$\left\{\begin{array}{l}{k+b=0}\\{b=1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$��
��ֱ��EF�Ľ���ʽΪ��y=-x+1��
�ߵ�P��a��b���Ƿ���������$y=\frac{1}{2x}$ͼ��ĵ㣬
��$b=\frac{1}{2a}$��
��E��a��1-a����F$��1-\frac{1}{2a}��\frac{1}{2a}��$��
��2����AOF���BOEһ�����ƣ�
��OA=OB=1��
��AB=$\sqrt{2}$����OBA=��OAB=45�㣬
��AE=$\sqrt{2}$AM=$\sqrt{2}$��1-a����BF=$\sqrt{2}$BN=$\sqrt{2}$��1-$\frac{1}{2a}$����
��BE=BA-AE=$\sqrt{2}$a��AF=BA-BF=$\frac{\sqrt{2}}{2a}$��
��BE•AF=$\frac{\sqrt{2}}{2a}$•$\sqrt{2}$a=1��
��OA•OB=1��
��BE•AF=OA•OB��
��$\frac{BE}{OB}=\frac{OA}{AF}$����OBA=��OAB=45�㣬
���AOF�ס�BEO��
��3����FOE=45��Ƕ�ʼ�ղ��䣮
�ߡ�AOF�ס�BEO��
���FOA=��OEB��
���FOE+��EOA=��EOA+��EAO��
�á�FOE=��EAO=45�㣮
���� �������ڷ����������ۺ��⣬�����˴���ϵ����һ�κ�������ʽ�����������ε��ж��������Լ����������������ʣ�ע�����ֱ��EF�Ľ���ʽ��֤��BE•AF=OA•OB=1�ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
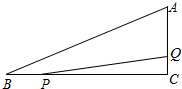 ��ͼ����Rt��ABC�У���C=90�㣬AC=5��BC=12������P�ӵ�B��ʼ�ر�BC���C��ÿ��2����λ���ȵ��ٶ��˶�������Q�ӵ�C��ʼ��C-A-B���B��ÿ��1����λ���ȵ��ٶ��˶�������PQ����P��Q�ֱ�ӵ�B��Cͬʱ��������P�㵽��C��ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��ͼ����Rt��ABC�У���C=90�㣬AC=5��BC=12������P�ӵ�B��ʼ�ر�BC���C��ÿ��2����λ���ȵ��ٶ��˶�������Q�ӵ�C��ʼ��C-A-B���B��ÿ��1����λ���ȵ��ٶ��˶�������PQ����P��Q�ֱ�ӵ�B��Cͬʱ��������P�㵽��C��ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x-4 | B�� | 3x2-4 | C�� | 3x2-4x | D�� | 4x-4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����?ABCD�У�AEƽ�֡�BAD��DC�ڵ�E��AD=5cm��AB=8cm��
��ͼ����?ABCD�У�AEƽ�֡�BAD��DC�ڵ�E��AD=5cm��AB=8cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20��15 | B�� | 15��20 | C�� | 25��10 | D�� | 10��25 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
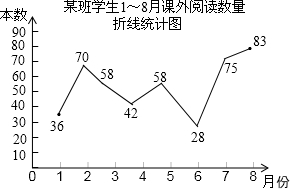 ЦЦͳ����3�·�ij��ȫ��8�����еĿ�������ָ����������������ͳ��ͼ����ͼ��������8�����еĿ�������ָ������λ���ǣ�������
ЦЦͳ����3�·�ij��ȫ��8�����еĿ�������ָ����������������ͳ��ͼ����ͼ��������8�����еĿ�������ָ������λ���ǣ�������| A�� | 59 | B�� | 58 | C�� | 50 | D�� | 42 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com