
����������9�֣�ij�̼Ҽƻ��ӳ��Ҳɹ��յ��ͱ������ֲ�Ʒ��20̨���յ��IJɹ����� ��Ԫ/̨����ɹ�����
��Ԫ/̨����ɹ����� ��̨������
��̨������ ��
�� ��
�� Ϊ������������IJɹ�����
Ϊ������������IJɹ����� ��Ԫ/̨����ɹ�����
��Ԫ/̨����ɹ����� ��̨������
��̨������ ��
�� ��
�� ��������
��������
��1�����̼��볧��Э�̣��ɹ��յ������������ڱ��������� ���ҿյ��ɹ����۲�����1200Ԫ���ʸ��̼ҹ��м��ֽ���������
���ҿյ��ɹ����۲�����1200Ԫ���ʸ��̼ҹ��м��ֽ���������
��2�����̼ҷֱ���1760Ԫ��̨��1700Ԫ��̨�����۵����۳��յ��ͱ��䣬��ȫ�����꣮�ڣ�1���������£��ʲɹ��յ�����̨ʱ������������������
��1��5����2��15��10650��
��������
�����������1����յ��IJɹ�����Ϊx̨�������IJɹ�����Ϊ��20��x��̨��Ȼ����������͵����г�����ʽ�飬���õ�x��ȡֵ��Χ���ٸ��ݿյ�̨����������ȷ������������
��2����������ΪWԪ��������������ڿյ��ͱ��������֮�������õ�W��x�ĺ�����ϵʽ�������ɶ���ʽ��ʽ��Ȼ����ݶ��κ�����������������ֵ���ɣ�
�����������1����յ��IJɹ�����Ϊx̨�������IJɹ�����Ϊ��20��x��̨��
������ã� ��
��
�ⲻ��ʽ�ٵã�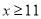 ��
��
�ⲻ��ʽ�ڵã�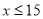 ��
��
���ԣ�����ʽ��Ľ⼯�� ��
��
��x��������
��x��ȡ��ֵΪ11��12��13��14��15��
���ԣ����̼ҹ���5�ֽ���������
��2����������ΪWԪ���յ��IJɹ�����Ϊx̨��
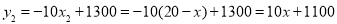 ��
��
��W=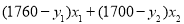 =
=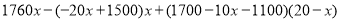
=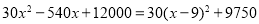 ��
��
��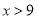 ʱ��W��x�����������
ʱ��W��x�����������
�� ��
��
�൱x=15ʱ��W���ֵ=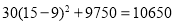 ��Ԫ����
��Ԫ����
�𣺲ɹ��յ�15̨ʱ���������������������ֵΪ10650Ԫ��
���㣺1�����κ�����Ӧ�ã�2��һԪһ�β���ʽ���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ̩���н��������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
ij��վ��С�ӱߣ��Ӻ����Ͽ����Ӷ����͵���������ʾ��ʱ�䣬�������ͼ��ʾ����õ�������ʾ��ʵ��ʱ���� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����������10�֣���ͼ���ڡ�ABC�У���B���C��ƽ���߽��ڵ�O����O��һֱ�߽�AB��AC��E��F����BE=EO.���ABC���ܳ��ȡ�AEF���ܳ���12cm��O��AB�ľ���Ϊ4cm�����OBC�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����и��������꼶��ѧ������������ѧ�Ծ��������棩 ���ͣ������
��ͼ��ʾ�������� ��
�� ����x���ཻ�ڵ�A��
����x���ཻ�ڵ�A�� ��0����B��
��0����B�� ��0������A�ڵ�B����࣮��
��0������A�ڵ�B����࣮�� ʱ��
ʱ�� 0���>����������<������
0���>����������<������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ̩�������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
ij��2014���ϰ��깫������Ԥ������ԼΪ23.07��Ԫ���������23.07�ھ�ȷ��__________λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�����и��������꼶��ѧ������������ѧ�Ծ��������棩 ���ͣ������
ij������һ�·��²�Ʒ���з��ʽ�ΪaԪ���Ժ�ÿ���²�Ʒ���з��ʽ���������������ʶ���x����ó��������·��²�Ʒ���з��ʽ�y��Ԫ������x�ĺ�����ϵʽΪy�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���е�ͽ�����꼶10�µ�����ѧ�Ծ��������棩 ���ͣ������
��8�֣���ͼ����֪AC��BC��BD��AD��AC��BD����O��AC��BD.��֤: (1)BC��AD; (2)��OAB�ǵ���������.
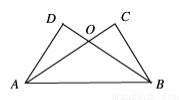
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���е�ͽ�����꼶10�µ�����ѧ�Ծ��������棩 ���ͣ������
��ͼ����֪��Rt��ABC�У���ACB=90�㣬��BAC=30�㣬��ֱ��AC���ҵ�P,ʹ��ABF�ǵ��������Σ����APB�Ķ���Ϊ .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��ͼ���ı���ABCD�������Σ�BE��BF��BE=BF��EF��BC���ڵ�G��

��1����֤��AE=CF��
��2������ABE=55�㣬���EGC�Ĵ�С��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com