
如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.

(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
(1)AE=CF (2)∠EGC=80°
【解析】
试题分析:(1)要证AE=CF,若我们能够证明其所在的三角形全等即可。AE位于
△AEB中,CF位于△CFB中,因为四边形ABCD是正方形,则AB=BC,因为
BE⊥BF,则∠ABC=∠EBF=90°,都减去∠EBC,故∠ABE=∠CBF,又因为BE=BF,故可以
由SAS定理得到两个三角形全等。故AE=CF。
(2)由三角形的外角等于和他不相邻的两个内角之和,则∠EGC=∠EBG+∠BEF,由BE⊥BF,
∠FBE=90°,BE=BF,则∠BEF=∠EFB=45°,而∠EBG=90°-∠ABE=90°-55°=35°,故可求出∠EGC=80°。
试题解析:
(1)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC, 1分
∵BE⊥BF,
∴∠FBE=90°,
∵∠ABE+∠EBC=90°,∠CBF+∠EBC=90°,
∴∠ABE=∠CBF, 2分
在△AEB和△CFB中,

∴△AEB≌△CFB(SAS), 4分
∴AE=CF. .5分
(2)【解析】
∵BE⊥BF,
∴∠FBE=90°,
又∵BE=BF,
∴∠BEF=∠EFB=45°,
∵四边形ABCD是正方形,
∴∠ABC=90°,
又∵∠ABE=55°,
∴∠EBG=90°-55°=35°, 7分
∴∠EGC=∠EBG+∠BEF=45°+35°=80° 9分
考点:1.三角形全等的判定定理 2.正方形的性质 3.角形的外角等于和他不相邻的两个内角之和


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市高新区九年级上学期期中联考数学试卷(解析版) 题型:解答题
(本题满分9分)某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价 (元/台)与采购数量
(元/台)与采购数量 (台)满足
(台)满足 (
( ,
, 为整数);冰箱的采购单价
为整数);冰箱的采购单价 (元/台)与采购数量
(元/台)与采购数量 (台)满足
(台)满足 (
( ,
, 为整数).
为整数).
(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的 ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?
(2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省靖江市共同体九年级上学期期中考试数学试卷(解析版) 题型:选择题
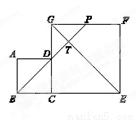
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )
A.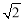 B.
B.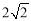 C.2 D.1
C.2 D.1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省靖江市共同体九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题8分)如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省上学期九年级第一次段考数学试卷(解析版) 题型:填空题
在一个不透明的口袋中有3个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球实验后发现,摸到红球的频率稳定在15%左右,则口袋中的白球大约有_________个。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省八年级上学期期中考试数学试卷(解析版) 题型:解答题
已知:点B.F.C.E在同一条直线上,FB=CE,AC=DF,现给出下列条件:①AB=ED;②∠A=∠D=90°;③∠ACB=∠DFE.请你从上面三个条件中选择一个合适的条件,添加到已知条件中,使得AB∥ED成立,并给出证明.

答:我选择的条件是: ;
我的证明过程如下:
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省上学期九年级第一次段考数学试卷(解析版) 题型:解答题
(6分)如图,正方形ABCD中,E、F分别是AB、BC边上的点,且AE=BF,求证:AF⊥DE。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com