
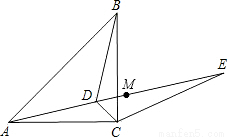
(10分)如图所示,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证: ME=BD.
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)由等腰直角△ABC,可证△BDC≌△ADC,得∠DCA=∠DCB=45o,然后求证∠BDM=∠EDC即可.
(2)连接MC,可知△MDC是等边三角形,可求证∠EMC=∠ADC。再△ADC≌△EMC即可.
(1)在等腰直角△ABC中,
∵∠CAD=∠CBD=15o,
∴∠BAD=∠ABD=45o-15o=30o. ∴BD=AD.
又∵CA=CB,∴△BDC≌△ADC(SAS).∴∠DCA=∠DCB.
又∵∠ACB=90o,∴∠DCA=∠DCB=45o.
∵∠BDM=∠ABD+∠BAD=30o+30o=60o,∠EDC=∠DAC+∠DCA=15o+45o=60o,
∴∠BDM=∠EDC. ∴DE平分∠BDC.
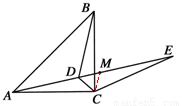
(2)如图,连接MC.
∵DC=DM,且∠MDC=60°,∴△MDC是等边三角形,即CM=CD.
又∵∠EMC=180°-∠DMC=180°-60°=120°,∠ADC=180°-∠MDC=180°-60°=120°,
∴∠EMC=∠ADC.
又∵CE=CA,∴∠DAC=∠CEM=15°.
∴△ADC≌△EMC(AAS).∴ME=AD=BD.
考点:1.等腰(直角)三角形的性质;2.全等三角形的判定和性质;3.等边三角形的判定和性质;4.三角形内角和定理.


科目:初中数学 来源:2015届河北省唐山市八年级下学期期末考数学试卷(解析版) 题型:解答题
某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了部分学生进行调查。对数据进行整理,得到下面两个都不完整的扇形统计图(图1)和条形统计图(图2):
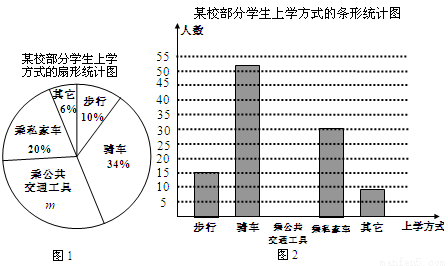
(1)该校数学兴趣小组采取的调查方式是 (填“普查”或“抽样调查”);一共调查了 名学生;
(2)求扇形统计图中的m,并补全条形统计图;
(3)求扇形统计图中,“乘私家车”所对应扇形的圆心角的度数;
(4)小明说:“为了调查方便,全部在同一个年级抽取.” 这样的抽样是否合理?请说明理由;
(5)根据调查的结果,估计全校2000名学生骑车上学有多少人?
查看答案和解析>>
科目:初中数学 来源:2015届江西省高安市八年级下学期期末考试数学试卷(解析版) 题型:选择题
如图,大正方形中有2个小正方形,如果它们的面积分别是S1、S2,那么S1、S2的大小关系是( )
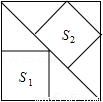
A.S1>S2 B.S1=S2
C.S1<S2 D.S1、S2的大小关系不确定
查看答案和解析>>
科目:初中数学 来源:2015届江西省九年级上学期入学考试数学试卷(解析版) 题型:选择题
如图,已知点D、E、F分别是△ABC边AB、AC、BC的中点,设△ADE和△BDF的周长分别为L1和L2,则L1和L2的大小关系是( ).
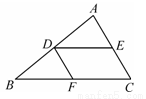
A.L1=L2 B.L1<L2
C.L1>L2 D.L1与L2的大小关系不确定
查看答案和解析>>
科目:初中数学 来源:2015届江西省八年级下学期第一次月考数学试卷(解析版) 题型:解答题
(8分)如图所示,已知∠1=∠2,AB=AD, ∠B=∠D=90º,请判断△AEC的形状,并说明理由.
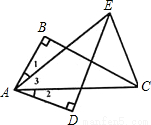
查看答案和解析>>
科目:初中数学 来源:2015届江西省八年级下学期第一次月考数学试卷(解析版) 题型:填空题
如图所示,O是△ABC的∠ABC.∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC = 10,则△ODE的周长为 .
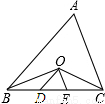
查看答案和解析>>
科目:初中数学 来源:2015届江西省吉安市六校八年级下学期联考数学试卷(解析版) 题型:解答题
设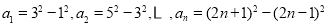 。(n为大于0的自然数)
。(n为大于0的自然数)
(1)探究an是否为8的倍数。
(2)若一个数的算术平方根是一个自然数,则称这个数是“完全平方数”,如:1,4,9就是完全平方数。试找出a1,a2,…,an,…,这一列数中从小到大排列的前4个完全平方数,并指出当n满足什么条件时,an为完全平方数。(不必说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com