
【题目】为弘扬中华优秀传统文化,某校组织了“古诗词”知识竞赛,由九年级的若干名学生参加选拔赛,从中选出10名优胜者,下面是对参赛学生成绩的不完整统计.
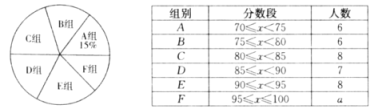
(1)统计表中,![]() =_____;各组人数的中位数是_____;统计图中,
=_____;各组人数的中位数是_____;统计图中,![]() 组所在扇形的圆心角是_____°;
组所在扇形的圆心角是_____°;
(2)李明同学得了88分,他说自己在参加选拔赛的同学中属于中午偏上水平,你认为他说的有道理吗?为什么?
(3)选出的10名优胜者中,男生、女生的分布情况如下表.
一班 | 二班 | 三班 | 四班 | 五班 | 六班 | |
男生人数 | 1 | 1 | 2 | 1 | 0 | 0 |
女生人数 | 1 | 0 | 0 | 2 | 1 | 1 |
若从中任选1名男生和1名女生代表学校参加全区的比赛,请有列表法或画树状图法求男生和女生都出在四班的概率.
【答案】(1)5,6.5,72;(2)有道理.理由见解析;(3)选出的男生和女生都来自四班的概率是![]() .
.
【解析】
(1)根据A组人数占总人数的15%求得总人数,再用总人数减去A、B、C、D、E五组的人数边求得a的值;把各组人数按由少到多排列便能求出各组人数的中位数;先求C组人数占总人数的百分比,再用360°乘以这个百分比便能求得![]() 组所在扇形的圆心角;
组所在扇形的圆心角;
(2)根据85分以下的有20人占50%,再用85与之比较即可;
(3)用列表法列举出所有可能出现的结果数,从中找出男生和女生都出在四班的结果数,进而求出概率.
解:(1)6÷15%=40(人)
40-6-6-8-7-8=5(人)
故a=5,
六组人数按照由少到多的顺序排列为:5,6,6,7,8,8,
故各组人数的中位数是![]() ,
,
![]() 组所在扇形的圆心角是360°×
组所在扇形的圆心角是360°×![]() 72°,
72°,
故答案为:5,6.5,72;
(2)正确.
理由:参加选拔赛的共有40人,85分以下的有20人占50%,他得了88分,可以说是中等偏上水平.
(3)由题意可知10名优胜者中,男生、女生各5名.
用![]() 代表男生,其中四班男生为
代表男生,其中四班男生为![]() ,用
,用![]() 代表女生,其中
代表女生,其中![]() 为四班女生,列表如下:
为四班女生,列表如下:
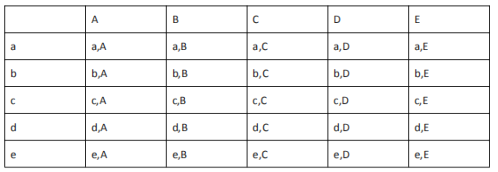
由表格可知,共有25种等可能的情况,其中选出的一男一女都来自四班的情况有2种,
故选出的男生和女生都来自四班的概率是![]() .
.


科目:初中数学 来源: 题型:
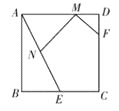
【题目】如图,在正方形ABCD中,AB=4,E是BC边的中点, F是CD边上的一点, 且DF=1.若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽泰州”的工作部署,市政府计划对城区道路进行改造,现安排甲、乙两个工程队完成该改造工作.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造720米的道路比乙队改造同样长的道路少用4天.
倍,甲队改造720米的道路比乙队改造同样长的道路少用4天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,若需改造的道路全长2400米,改造总费用不超过195万元,则至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,BC为⊙O直径,延长AC至D,过D作⊙O切线,切点为E,且∠D=90°,连接BE.DE=12,
(1)若CD=4,求⊙O的半径;
(2)若AD+CD=30,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,其中
两点,其中![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴交
,抛物线的对称轴交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() ,连接
,连接![]() .
.
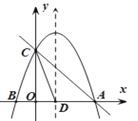
(1)求抛物线和直线![]() 的解析式:
的解析式:
(2)若抛物线上存在一点![]() ,使
,使![]() 的面积是
的面积是![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标;
的坐标;
(3)在抛物线的对称轴上是否存在一点![]() ,使线段
,使线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到线段
得到线段![]() ,且
,且![]() 恰好落在抛物线上?若存在,求出点
恰好落在抛物线上?若存在,求出点![]() 的坐标;若不存在,请说叫理由.
的坐标;若不存在,请说叫理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
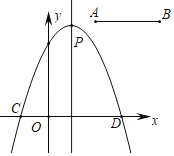
【题目】如图,线段AB,A(2,3),B(5,3),抛物线y=﹣(x﹣1)2﹣m2+2m+1与x轴的两个交点分别为C,D(点C在点D的左侧)
(1)求m为何值时抛物线过原点,并求出此时抛物线的解析式及对称轴和项点坐标.
(2)设抛物线的顶点为P,m为何值时△PCD的面积最大,最大面积是多少.
(3)将线段AB沿y轴向下平移n个单位,求当m与n有怎样的关系时,抛物线能把线段AB分成1:2两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
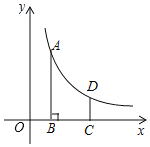
【题目】如图,反比例函数y=![]() (x>0)的图象上一点A(m,4),过点A作AB⊥x轴于B,CD∥AB,交x轴于C,交反比例函数图象于D,BC=2,CD=
(x>0)的图象上一点A(m,4),过点A作AB⊥x轴于B,CD∥AB,交x轴于C,交反比例函数图象于D,BC=2,CD=![]() .
.
(1)求反比例函数的表达式;
(2)若点P是y轴上一动点,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点O为坐标原点,直线![]() 交x轴于点A,交y轴于点B,点D在直线AB上,点D的纵坐标为6,点C在x轴上且位于原点右侧,连接CD,且
交x轴于点A,交y轴于点B,点D在直线AB上,点D的纵坐标为6,点C在x轴上且位于原点右侧,连接CD,且![]() .
.

![]() 如图1,求直线CD的解析式;
如图1,求直线CD的解析式;
![]() 如图2,点P在线段AB上
如图2,点P在线段AB上![]() 点P不与点A,B重合
点P不与点A,B重合![]() ,过点P作
,过点P作![]() 轴,交CD于点Q,点E是PQ的中点,设P点的横坐标为t,EQ的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
轴,交CD于点Q,点E是PQ的中点,设P点的横坐标为t,EQ的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
![]() 如图3,在
如图3,在![]() 的条件下,以CQ为斜边作等腰直角
的条件下,以CQ为斜边作等腰直角![]() ,且点M在直线CD的右侧,连接OE,OM,当
,且点M在直线CD的右侧,连接OE,OM,当![]() 时,求点M的坐标.
时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数.按此规律推算出正方形A10B10C10D10四条边上的整点共有______个.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com