
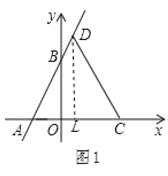
【题目】已知:在平面直角坐标系中,点O为坐标原点,直线![]() 交x轴于点A,交y轴于点B,点D在直线AB上,点D的纵坐标为6,点C在x轴上且位于原点右侧,连接CD,且
交x轴于点A,交y轴于点B,点D在直线AB上,点D的纵坐标为6,点C在x轴上且位于原点右侧,连接CD,且![]() .
.

![]() 如图1,求直线CD的解析式;
如图1,求直线CD的解析式;
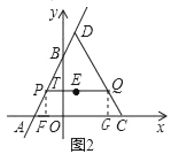
![]() 如图2,点P在线段AB上
如图2,点P在线段AB上![]() 点P不与点A,B重合
点P不与点A,B重合![]() ,过点P作
,过点P作![]() 轴,交CD于点Q,点E是PQ的中点,设P点的横坐标为t,EQ的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
轴,交CD于点Q,点E是PQ的中点,设P点的横坐标为t,EQ的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
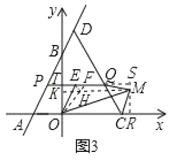
![]() 如图3,在
如图3,在![]() 的条件下,以CQ为斜边作等腰直角
的条件下,以CQ为斜边作等腰直角![]() ,且点M在直线CD的右侧,连接OE,OM,当
,且点M在直线CD的右侧,连接OE,OM,当![]() 时,求点M的坐标.
时,求点M的坐标.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)A、D两点在直线y=2x+4上,可依条件建立方程求得坐标,再根据等腰三角形性质求得点C坐标,应用待定系数法求直线CD解析式;
(2)点P在线段AB上,可得P(t,2t+4),根据PQ∥x轴,可得P与Q纵坐标相等,求得Q(-t+2,2t+4),根据E为PQ中点,可得d=EQ=12PQ=-t+1;
(3)过M作SR⊥x轴于R,交PQ延长线于S,利用等腰三角形两腰相等构造全等三角形,在TQ上截取TF=OT,构造等腰Rt△TOF,应用相似三角形判定和性质,建立方程求解.
(1)如图1,
直线y=2x+4经过点A,D,
当y=0时,x=-2,
∴A(-2,0),
当y=6时,x=1,
∴D(1,6),
过点D作DL⊥x轴于点L,
∴L(1,0),
∴AL=3,
∵AD=CD,
∴AL=CL=3,
∴OC=1+3=4,
∴C(4,0),
设直线CD的解析式为y=kx+b,将C(4,0),D(1,6)代入得
![]() ,
,
解得k=-2,b=8,
∴直线CD的解析式为y=-2x+8;
(2)如图2,过点P,Q分别作PF⊥x轴于点F,QG⊥x轴于点G,PQ交y轴于点T,
∵点P在直线y=2x+4上且点P的横坐标为t,
∴点P的坐标为(t,2t+4),
∵PQ∥z轴,
∴∠OTQ=∠AOT=90°,
∴PQ⊥y轴,
∴OT=2t+4,
∴点Q的纵坐标为2t+4,
点Q在直线y=-2x+8上,当y=2t+4时,2t+4=-2x+8,解得x=-2t+2,
∴点Q的坐标为(-t+2,2t+4),
∵∠PFC=∠QGC=90°
∴PF∥QG
又∵PQ∥FG
∴四边形PFGQ为平行四边形
∴PQ=FG=(-t+2)-t=-2t+2
∵E为PQ的中点
∴EP=EQ=![]() PQ=
PQ=![]() (-2t+2)=-t+1
(-2t+2)=-t+1
∴d=-t+1 (-1<t<0);
(3)如图3,过点M作x轴的垂线,垂足为R,交PQ的延长线于点S,
∵∠CMQ=90°,CM=MQ
∴∠QCM=45°
在△OCM中,∠COM+∠OMC+∠OCM=180°
∴(90°-∠BCE-∠ECM)+(90°-∠OMQ)+(∠ACD+45°)=180°
∴∠EOM=45°
令CR=m,
∵∠OTS=∠TOR=∠ORS=90°
∴四边形ORST是矩形
∴RS=OT=2t+4,TS=OR=m+4
∴QS=m+4-(-t+2)=m+t+2
∵CM=QM,∠CRM=∠MSQ=90°,∠MCR=90°-∠CMR=∠QMS
∴△QMS≌△MCR
∴MS=CR=m,MR=QS=m+t+2
∵MS+MR=RS
∴m+m+t+2=2t+4
∴m=![]() t+1
t+1
∴MR=![]() t+3,OR=
t+3,OR=![]() t+5
t+5
在TQ上截取TF=OT=2t+4,连接OF,过点E作EH⊥OF于点H,
则∠COF=∠TFO=45°,OF=![]() OT=
OT=![]() (2t+4),EF=FT-ET=2t+4-(-t+1+t)=2t+3,EH=FH=
(2t+4),EF=FT-ET=2t+4-(-t+1+t)=2t+3,EH=FH=![]() EF=
EF=![]() (2t+3),
(2t+3),
∴OH=OF-FH=![]() (2t+4)-
(2t+4)-![]() (2t+3)=
(2t+3)=![]() (2t+5),
(2t+5),
∵∠MOR=45°-∠FOM=∠EOH
∴tan∠MOR=tan∠EOH
在Rt△MOR中,tan∠MOR=![]() ,在Rt△OEH中,tan∠EOH=
,在Rt△OEH中,tan∠EOH=![]() ,
,
∴![]()
∴MROH=OREH
∴![]()
![]()
解得![]() (舍去)
(舍去)
∴![]()
过点M作MK⊥y轴于点K,可证四边形ORMK是矩形
∴![]()
∴点M的坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】某校准备组织一次“研学之旅”活动,现用抽签的方式从以下四个地方:九峰公园、柑橘博览园、平田桐树坑、长潭水库(其中九峰公园、平田桐树坑是爱国主义教育基地)中确定两个作为活动地点.将四个地点分别写在4张完全相同的卡片上,背面朝上并洗匀,先从中随机抽取一张卡片,再从剩下的卡片中随机抽取一张.则“抽中的两个地方都是爱国主义教育基地”的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校组织了“古诗词”知识竞赛,由九年级的若干名学生参加选拔赛,从中选出10名优胜者,下面是对参赛学生成绩的不完整统计.
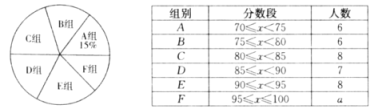
(1)统计表中,![]() =_____;各组人数的中位数是_____;统计图中,
=_____;各组人数的中位数是_____;统计图中,![]() 组所在扇形的圆心角是_____°;
组所在扇形的圆心角是_____°;
(2)李明同学得了88分,他说自己在参加选拔赛的同学中属于中午偏上水平,你认为他说的有道理吗?为什么?
(3)选出的10名优胜者中,男生、女生的分布情况如下表.
一班 | 二班 | 三班 | 四班 | 五班 | 六班 | |
男生人数 | 1 | 1 | 2 | 1 | 0 | 0 |
女生人数 | 1 | 0 | 0 | 2 | 1 | 1 |
若从中任选1名男生和1名女生代表学校参加全区的比赛,请有列表法或画树状图法求男生和女生都出在四班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图像过点
的图像过点![]() ,顶点为
,顶点为![]()
![]() 求
求![]() 的值.
的值.
![]() 点
点![]() 以点
以点![]() 为旋转中心,顺时针旋转
为旋转中心,顺时针旋转![]() 得到点
得到点![]() ,判断点
,判断点![]() 是否落在抛物线上.
是否落在抛物线上.
![]() 第一象限内抛物线上有一点
第一象限内抛物线上有一点![]() 与
与![]() 相交于点
相交于点![]() ,当
,当![]() 时,求点
时,求点![]() 坐标.
坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丁老师为了解所任教的两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成 5 组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
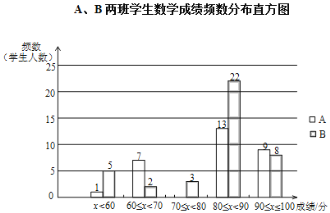
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A 班:80 80 82 83 85 85 86 87 87 87 88 89 89
B 班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息,请写出表中 m、n的值____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
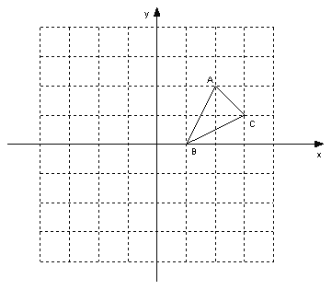
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1,
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴并写出对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六![]() 一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
![]() 求A、B两种品牌服装每套进价分别为多少元?
求A、B两种品牌服装每套进价分别为多少元?
![]() 该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com