
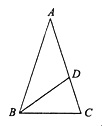
【题目】如图,在△ABC中,AB=AC=1,BC=![]() ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断![]() 与AC·CD 的大小关系;
与AC·CD 的大小关系;
(2)求∠ABD 的度数.
【答案】(1)、![]() ;(2)、36°.
;(2)、36°.
【解析】
试题分析:(1)、通过计算得到![]() =
=![]() ,再计算AC·CD,比较即可得到结论;(2)、由
,再计算AC·CD,比较即可得到结论;(2)、由![]() ,得到
,得到![]() , 即
, 即![]() , 从而得到△ABC∽△BDC, 故有
, 从而得到△ABC∽△BDC, 故有![]() , 从而得到BD=BC=AD,故∠A=∠ABD, ∠ABC=∠C=∠BDC. 设∠A=∠ABD=x,则∠BDC=2x,∠ABC=∠C=∠BDC=2x, 由三角形内角和等于180°, 解得:x=36°, 从而得到结论.
, 从而得到BD=BC=AD,故∠A=∠ABD, ∠ABC=∠C=∠BDC. 设∠A=∠ABD=x,则∠BDC=2x,∠ABC=∠C=∠BDC=2x, 由三角形内角和等于180°, 解得:x=36°, 从而得到结论.
试题解析:(1)、∵AD=BC=![]() , ∴
, ∴![]() =
=![]() =
=![]() . ∵AC=1,
. ∵AC=1,
∴CD=![]() =
=![]() , ∴
, ∴![]() ;
;
(2)、∵![]() , ∴
, ∴![]() , 即
, 即![]() , 又∵∠C=∠C,∴△ABC∽△BDC, ∴
, 又∵∠C=∠C,∴△ABC∽△BDC, ∴![]() , 又∵AB=AC, ∴BD=BC=AD, ∴∠A=∠ABD,∠ABC=∠C=∠BDC. 设∠A=∠ABD=x, 则∠BDC=∠A+∠ABD=2x, ∴∠ABC=∠C=∠BDC=2x, ∴∠A+∠ABC+∠C=x+2x+2x=180°, 解得:x=36°,∴∠ABD=36°.
, 又∵AB=AC, ∴BD=BC=AD, ∴∠A=∠ABD,∠ABC=∠C=∠BDC. 设∠A=∠ABD=x, 则∠BDC=∠A+∠ABD=2x, ∴∠ABC=∠C=∠BDC=2x, ∴∠A+∠ABC+∠C=x+2x+2x=180°, 解得:x=36°,∴∠ABD=36°.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】已知a、b、c 为三正整数,且a、b的最大公因子为12,a、c的最大公因子为18.若a介于50与100之间,则下列叙述何者正确?( )
A.8是a的因子,8是b的因子
B.8是a的因子,8不是b的因子
C.8不是a的因子,8是c的因子
D.8不是a的因子,8不是c的因子
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学游戏中,老师在A、B、C三个盘子里分别放了一些糖果,糖果数依次为a0、b0、c0 , 记为G0=(a0 , b0 , c0).游戏规则如下:若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作.若三个盘子中的糖果数都相同,游戏结束.n次操作后的糖果数记为Gn=(an , bn , cn).小明发现:若G0=(4,8,18),则游戏永远无法结束,那么G2016= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtΔABC中,∠C=90,AC=4cm,BC=3cm.动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动。连接PM、PN。设移动时间为t(单位:秒,0<t<2.5).
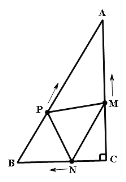
(1)当t为何值时,以A、P、M为顶点的三角形与ΔABC相似?
(2)是否存在某一时刻t,使△PMN 的面积恰好是△ABC 面积的![]() ;若存在求t的值;若不存在,请说明理由.
;若存在求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上每相邻两点间的距离为一个单位长度,点A、B、C、D对应的数分别是a、b、c、d,且d﹣2a=14 ![]()
(1)那么a= , b=;
(2)点A以3个单位/秒的速度沿着数轴的正方向运动,1秒后点B以4个单位/秒的速度也沿着数轴的正方向运动.当点A到达D点处立刻返回,与点B在数轴的某点处相遇,求这个点对应的数;
(3)如果A、B两点以(2)中的速度同时向数轴的负方向运动,点C从图上的位置出发也向数轴的负方向运动,且始终保持AB= ![]() AC.当点C运动到﹣6时,点A对应的数是多少?
AC.当点C运动到﹣6时,点A对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)16+(﹣25)+24+(﹣35)
(2)(﹣ ![]() )×(﹣1
)×(﹣1 ![]() )÷(﹣2
)÷(﹣2 ![]() )
)
(3)23×(﹣5)﹣(﹣3)÷ ![]()
(4)|﹣10|+|(﹣4)2﹣(1﹣32)×2|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个矩形的一边长是某个正方形边长的2倍,另一边长比该正方形边长少1厘米,且矩形的面积比该正方形的面积大8平方厘米,那么该正方形的边长是_____厘米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com