
分析 根据分针每分钟转6°,时针每分钟转0.5°得到45分钟分针从数字12开始转的度数,时针从数字3开始转的度数,得到时针与分针的夹角,根据补角的概念计算即可.
解答 解:3时45分时,分针从数字12开始转了45×6°=270°,时针从数字3开始转了45×0.5°=22.5°
所以3时40分时,时针与分针所夹的角度=270°-22.5°-3×30°=157.5°,
180°-157.5°=22.5°,
则时针与分针的夹角的补角为22.5°,
故答案为:22.5°.
点评 本题考查的是余角和补角的概念、钟面角的确定,掌握钟面被分成12大格,每大格30°;分针每分钟转6°,时针每分钟转0.5°是解题的关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
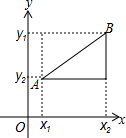 阅读材料
阅读材料查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
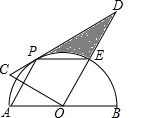 如图,在Rt△COD中,∠COD=90°,∠D=30°,斜边CD与以AB为直径,O为圆心的半圆相切于点P,OD与半圆交于点E,连接PA,PE,PA与OC交于点F.
如图,在Rt△COD中,∠COD=90°,∠D=30°,斜边CD与以AB为直径,O为圆心的半圆相切于点P,OD与半圆交于点E,连接PA,PE,PA与OC交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com