
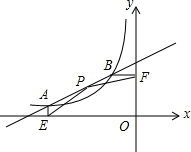
 如图,函数y=$\frac{k}{x}$(x<0)的图象与直线y=$\frac{1}{2}$x+m相交于点A和点B.过点A作AE⊥x轴于点E,过点B作BF⊥y轴于点F,P为线段AB上的一点,连接PE、PF.若△PAE和△PBF的面积相等,且xP=-$\frac{5}{2}$,xA-xB=-3,则k的值是( )
如图,函数y=$\frac{k}{x}$(x<0)的图象与直线y=$\frac{1}{2}$x+m相交于点A和点B.过点A作AE⊥x轴于点E,过点B作BF⊥y轴于点F,P为线段AB上的一点,连接PE、PF.若△PAE和△PBF的面积相等,且xP=-$\frac{5}{2}$,xA-xB=-3,则k的值是( )| A. | -5 | B. | $-\frac{7}{2}$ | C. | -2 | D. | -1 |
分析 由题意可得xA、xB是方程$\frac{k}{x}$=$\frac{1}{2}$x+m即x2+2mx-2k=0的两根,根据根与系数的关系可得xA+xB=-2m,xA•xB=-2k.易得xA•yA=xB•yB=k,由S△PAE=S△PBF可求出yP,然后把点P的坐标代入y=$\frac{1}{2}$x+m就可求出m,再根据xA-xB=-3就可求出k的值.
解答 解:由题意可得:xA、xB是方程$\frac{k}{x}$=$\frac{1}{2}$x+m即x2+2mx-2k=0的两根,
∴xA+xB=-2m,xA•xB=-2k.
∵点A、B在反比例函数y=$\frac{k}{x}$的图象上,
∴xA•yA=xB•yB=k.
∵S△PAE=S△PBF,
∴$\frac{1}{2}$yA(xP-xA)=$\frac{1}{2}$(-xB)(yB-yP),
整理得xP•yA=xB•yP,
∴-$\frac{5}{2}$$\frac{k}{{x}_{A}}$=xB•yP,
∴-$\frac{5}{2}$k=xA•xB•yP=-2kyP,.
∵k≠0,
∴yP=$\frac{5}{4}$,
∴$\frac{1}{2}$×(-$\frac{5}{2}$)+m=$\frac{5}{4}$,
∴m=$\frac{5}{2}$.
∵xA-xB=-3,
∴(xA-xB)2=(xA+xB)2-4xA•xB=(-2×$\frac{5}{2}$)2+8k=9,
∴k=-2.
故选C.
点评 本题主要考查了运用待定系数法求直线的解析式、根与系数的关系、完全平方公式等知识,运用根与系数的关系是解决本题的关键.


科目:初中数学 来源: 题型:解答题
 如图,一辆汽车在直线形公路AB上由A向B行驶,M、N是分别位于公路两旁的村庄.
如图,一辆汽车在直线形公路AB上由A向B行驶,M、N是分别位于公路两旁的村庄.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=-2,y=-1 | B. | x=2,y=-1 | C. | x=-2,y=1 | D. | x=2,y=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
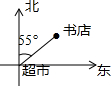 如图,书店在超市北偏东55°的方向上,那么以书店为参照点,超市的位置在( )
如图,书店在超市北偏东55°的方向上,那么以书店为参照点,超市的位置在( )| A. | 书店的南偏西55°的方向上 | B. | 书店的南偏东55°的方向上 | ||
| C. | 书店的南偏西35°的方向上 | D. | 书店的南偏东35°的方向上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com