
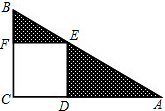
 如图所示,在△ABC中,∠ACB=90°,正方形CDEF的顶点E在斜边AB上,且AE=5,BE=8,则△ADE与△BEF的面积和为1780.
如图所示,在△ABC中,∠ACB=90°,正方形CDEF的顶点E在斜边AB上,且AE=5,BE=8,则△ADE与△BEF的面积和为1780. 分析 设正方形CDEF的边长为x,则EF=ED=x,则利用勾股定理表示出BF=$\sqrt{{8}^{2}-{x}^{2}}$,再证明Rt△BEF∽Rt△EAD,利用相似比求出x的值,则开始计算出S△BEF,然后利用相似三角形的性质计算出S△AED,从而得到△ADE与△BEF的面积和.
解答 解:设正方形CDEF的边长为x,则EF=ED=x,
所以BF=$\sqrt{{8}^{2}-{x}^{2}}$,
∵EF∥AC,
∴∠BEF=∠A,
∴Rt△BEF∽Rt△EAD,
∴BF:DE=BE:AE,即$\sqrt{{8}^{2}-{x}^{2}}$:x=8:5,解得x=$\frac{40\sqrt{89}}{89}$,
∴BF=$\frac{64\sqrt{89}}{89}$,
∴S△BEF=$\frac{1}{2}$BF•EF=$\frac{1}{2}$•$\frac{64\sqrt{89}}{89}$•$\frac{40\sqrt{89}}{89}$=1280,
∵$\frac{{S}_{△BEF}}{{S}_{△AED}}$=($\frac{8}{5}$)2,
∴S△AED=500,
∴△ADE与△BEF的面积和=1280+500=1780.
故答案为1780.
点评 本题考查了相似三角形的判定与性质:.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了正方形的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
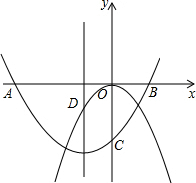 如图,在平面直角坐标系xOy中,把抛物线C1:y=-x2沿x轴翻折,再平移得到抛物线C2,恰好经过点A(-3,0)、B(1,0),抛物线C2与y轴交于点C,抛物线C1:y=-x2与抛物线C2的对称轴交于D点.
如图,在平面直角坐标系xOy中,把抛物线C1:y=-x2沿x轴翻折,再平移得到抛物线C2,恰好经过点A(-3,0)、B(1,0),抛物线C2与y轴交于点C,抛物线C1:y=-x2与抛物线C2的对称轴交于D点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
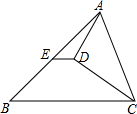 如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为( )
如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为( )| A. | 1 | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某地4月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )
某地4月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )| A. | 19,19 | B. | 19,19.5 | C. | 21,22 | D. | 20,20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com