
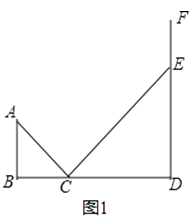
【题目】已知:如图,∠B=90°,AB∥DF,AB=4cm,BD=10cm,点C是线段BD上一动点,点E是直线DF上一动点,且始终保持AC⊥CE. 
(1)如图1试说明:∠ACB=∠CED.
(2)若AC=CE,试求DE的长.
【答案】
(1)解:如图1,∵AB∥DF,∠B=90°,
∴∠EDC=180°﹣∠ABC=90°,
∴∠CED+∠ECD=90°,
∵AC⊥CE,
∴∠ACE=90°,
∴∠ACB+∠ECD=90°,
∴∠ACB=∠CED
(2)解:如图2,∵∠EDC=90°,∠B=90°,
∴∠B=∠EDC,
由(1)可得,∠ACB=∠CED,
在△ABC和△CDE中,
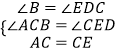 ,
,
∴△ABC≌△CDE,
∴DE=BC,AB=CD=4(cm),
∴BC=BD﹣CD=10﹣4=6(cm),
∴DE=6(cm)
【解析】(1)根据∠EDC=90°,得出∠CED+∠ECD=90°,再根据∠ACE=90°,得出∠ACB+∠ECD=90°,最后根据同角的余角相等,即可得出∠ACB=∠CED;(2)先判定△ABC≌△CDE,得出DE=BC,AB=CD=4(cm),进而得出BC=BD﹣CD=10﹣4=6(cm),根据全等三角形的对应边相等,即可得出DE=6(cm).


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两地相距450千米,一辆快车和一辆慢车上午7点分别从甲、乙两地以不变的速度同时出发开往乙地和甲地,快车到达乙地后休息一个小时按原速返回,快车返回甲地时已是下午5点,慢车在快车前一个小时到达甲地.试根据以上信息解答以下问题:
(1)分别求出快车、慢车的速度(单位:千米/小时);
(2)从两车出发直至慢车达到甲地的过程中,经过几小时两车相距150千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
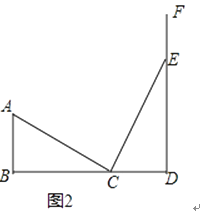
【题目】如图,在四边形ABCD中,∠B=90°,DE∥AB,DE交BC于E,交AC于F,DE=BC,∠CDE=∠ACB=30°. 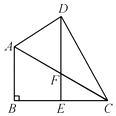
(1)若AB=4,求CD的长.
(2)判断△FCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;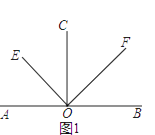
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;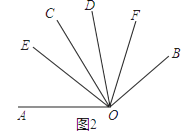
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= . (用含α与β的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD, CE=BD,求证: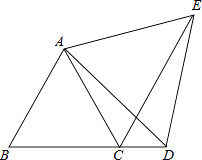
(1)△ABD≌△ACE;
(2)△ADE为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦节日期间,某商场为了促销,每件夹克按成本价提高50%后标价,后因季节关系按标价的8折出售,每件以168元卖出,这批夹克每件的成本价是( )
A.80元
B.84元
C.140元
D.100元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市民政部门举行“即开式福利彩票”销售活动,发行彩票10万张(每张彩票2元),在这些彩票中,设置如下奖项:
奖金(元) | 10000 | 5000 | 1000 | 500 | 100 | 50 |
数量(个) | 1 | 4 | 20 | 40 | 100 | 200 |
如果花2元购买1张彩票,那么所得奖金不少于1000元的概率是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com