
【题目】如图,在四边形ABCD中,∠B=90°,DE∥AB,DE交BC于E,交AC于F,DE=BC,∠CDE=∠ACB=30°. 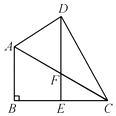
(1)若AB=4,求CD的长.
(2)判断△FCD的形状,并说明理由.
【答案】
(1)解:在△ACB和△CDE中,∠B=∠DEC=90°,BC=DE,
∠ACB=∠CDE,
在△ACB和△CDE中,
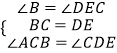 ,
,
∴△ACB≌△CDE,
∴AC=CD,
在Rt△ABC中,∠B=90°,∠ACB=30°,AB=4,
∴AC=2AB=8,
∴CD=8
(2)解:△FCD是等腰三角形,
理由:∵DE∥AB,∠B=90°,
∴∠DEC=90°,
∴∠DCE=90°﹣∠CDE=60°,
∴∠DCF=∠DCE﹣∠ACB=30°,
∴∠CDE=∠DCF,
∴DF=CF,
∴△FCD是等腰三角形
【解析】(1)证明△ACB≌△CDE,得到AC=CD,根据直角三角形的性质求出AC,求出CD;(2)根据等腰三角形的判定定理证明.
【考点精析】本题主要考查了等边三角形的判定的相关知识点,需要掌握三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6cm,BC=4cm,点P从点A出发(不含点A),沿A→B→C→D运动,同时,点Q从点B出发(不含点B),沿B→C→D运动,当点P到达点B时,点Q恰好到达点C,已知点P每秒比点Q每秒多运动1cm,当其中一点到达点D(不含点D)时,另一点停止运动.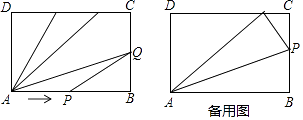
(1)求P、Q两点的速度;
(2)当其中一点到达点D时,另一点距离D点 cm(直接写答案);
(3)设点P、Q的运动时间为t(x),请用含t的代数式表示△APQ的面积为S(cm3),并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了运用平方差公式计算(x+2y﹣1)(x﹣2y+1),下列变形正确的是( )
A. [x﹣(2y+1)]2 B. [x+(2y﹣1)][x﹣(2y﹣1)]
C. [(x﹣2y)+1][(x﹣2y)﹣1] D. [x+(2y﹣1)]2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬一家人在2013年8月到北京旅游了4天,这4天的日期数(如8月1日的日期数为1)之和是38,则他们一家在北京旅游最后一天的日期数是( )
A.8号
B.9号
C.10号
D.11号
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明每天早晨在8时前赶到离家1千米的学校上学.一天,小明以80米/分的速度从家出发去学校,5分钟后,小明爸爸发现小明的语文书落在家里,于是,立即以180米/分的速度去追赶.则小明爸爸追上小明所用的时间为( )
A.2分钟
B.3分钟
C.4分钟
D.5分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B分别表示的数是6、-12、M、N、P为数轴上三个动点,它们同时都向右运动。点M从点A出发,速度为每秒2个单位长度,点N从点B出发,速度为点M的3倍,点P从原点出发,速度为每秒1个单位长度。![]()
(1)当运动3秒时,点M、N、P分别表示的数是、、;
(2)求运动多少秒时,点P到点M、N的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠B=90°,AB∥DF,AB=4cm,BD=10cm,点C是线段BD上一动点,点E是直线DF上一动点,且始终保持AC⊥CE. 
(1)如图1试说明:∠ACB=∠CED.
(2)若AC=CE,试求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校开展了以“梦想中国”为主题的摄影大赛,要求参赛学生每人交一件作品.现将从中挑选的50件参赛作品的成绩(单位:分)统计如下:
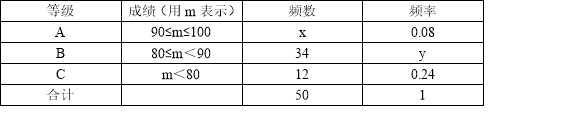
请根据上表提供的信息,解答下列问题:
(1)表中x的值为 ,y的值为 ;(直接填写结果)
(2)将本次参赛作品获得A等级的学生依次用A1、A2、A3…表示.现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,则恰好抽到学生A1和A2的概率为 .(直接填写结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com