
【题目】如图,点A、B分别表示的数是6、-12、M、N、P为数轴上三个动点,它们同时都向右运动。点M从点A出发,速度为每秒2个单位长度,点N从点B出发,速度为点M的3倍,点P从原点出发,速度为每秒1个单位长度。![]()
(1)当运动3秒时,点M、N、P分别表示的数是、、;
(2)求运动多少秒时,点P到点M、N的距离相等?
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )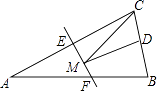
A.6
B.8
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌手机的进价为1200元,按原价的八折出售可获利14%,则该手机的原售价为( )
A.1800元
B.1700元
C.1710元
D.1750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.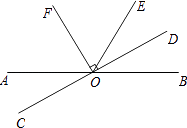
(1)若∠AOE=120°,求∠BOD的度数;
(2)写出图中所有与∠AOD互补的角: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=90°,DE∥AB,DE交BC于E,交AC于F,DE=BC,∠CDE=∠ACB=30°. 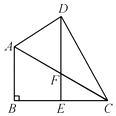
(1)若AB=4,求CD的长.
(2)判断△FCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何知识可以解决生活中许多距离最短的问题.让我们从书本一道习题入手进行知识探索.
(1)【回忆】
如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并说明理由.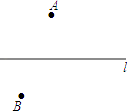
(2)【探索】
如图,A、B两个村庄在一条笔直的马路的两端,村庄 C在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置,并说明理由.
(3)如图,A、B、C、D四个村庄,现建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O的位置,并说明理由.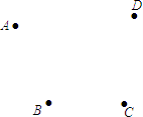
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;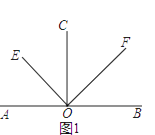
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;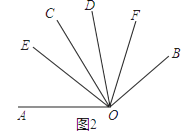
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= . (用含α与β的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦节日期间,某商场为了促销,每件夹克按成本价提高50%后标价,后因季节关系按标价的8折出售,每件以168元卖出,这批夹克每件的成本价是( )
A.80元
B.84元
C.140元
D.100元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com