
����Ŀ���ۺ���
��1����ͼ1����CO��AB������ΪO��OE��OF�ֱ�ƽ�֡�AOC���BOC�����EOF�Ķ�����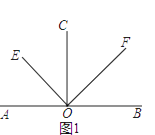
��2����ͼ2������AOC=��BOD=80�㣬OE��OF�ֱ�ƽ�֡�AOD���BOC�����EOF�Ķ�����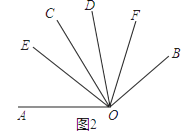
��3������AOC=��BOD=��������BOD�Ƶ�O��ת��ʹ������OC������OD�ļн�Ϊ�£�OE��OF�ֱ�ƽ�֡�AOD���BOC������+�¡�180�㣬�����£����EOC= �� ���ú�����µĴ���ʽ��ʾ��
���𰸡�
��1���⣺��CO��AB��
���AOC=��BOC=90�㣬
��OEƽ�֡�AOC��
���EOC= ![]() ��AOC=
��AOC= ![]() ��90��=45�㣬
��90��=45�㣬
��OFƽ�֡�BOC��
���COF= ![]() ��BOC=
��BOC= ![]() ��90��=45�㣬
��90��=45�㣬
��EOF=��EOC+��COF=45��+45��=90�㣻
��2���⣺��OEƽ�֡�AOD��
���EOD= ![]() ��AOD=
��AOD= ![]() ����80+�£�=40+
����80+�£�=40+ ![]() �£�
�£�
��OFƽ�֡�BOC��
���COF= ![]() ��BOC=
��BOC= ![]() ����80+�£�=40+
����80+�£�=40+ ![]() �£�
�£�
��COE=��EOD����COD=40+ ![]() �©���=40��
�©���=40�� ![]() �£�
�£�
��EOF=��COE+��COF=40�� ![]() ��+40+
��+40+ ![]() ��=80�㣻
��=80�㣻
��3��![]()
����������3����ͼ2���ߡ�AOC=��BOD=������COD=�£�
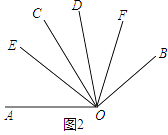
���AOD=��+�£�
��OEƽ�֡�AOD��
���DOE= ![]() ����+�£���
����+�£���
���COE=��DOE����COD= ![]() ��
��
��ͼ3���ߡ�AOC=��BOD=������COD=�£�
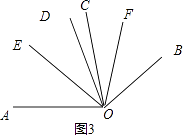
���AOD=��+�£�
��OEƽ�֡�AOD��
���DOE= ![]() �������£���
�������£���
���COE=��DOE+��COD= ![]() ��
��
���������� ![]() ��
��
���Դ��ǣ� ![]() ��
��
�����㾫�������ýǵ�ƽ���ߺͽǵ��������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪��һ���ǵĶ���������һ�����ߣ�������Ƿֳ�������ȵĽǣ��������߽�������ǵ�ƽ���ߣ���֮����Խ��мӼ����㣻һ���ǿ����������ǵĺͻ������ʾ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��һ������2013��8�µ�����������4�죬��4�������������8��1�յ�������Ϊ1��֮����38��������һ���ڱ����������һ����������ǣ� ��
A.8��
B.9��
C.10��
D.11��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�ֱ��ʾ������6��-12��M��N��PΪ�������������㣬����ͬʱ�������˶�����M�ӵ�A�������ٶ�Ϊÿ��2����λ���ȣ���N�ӵ�B�������ٶ�Ϊ��M��3������P��ԭ��������ٶ�Ϊÿ��1����λ���ȡ�![]()
��1�����˶�3��ʱ����M��N��P�ֱ��ʾ������������
��2�����˶�������ʱ����P����M��N�ľ�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�У���ȷ���ǣ� ��
A.|��0.1|��0
B.![]() ����|��
����|�� ![]() ?|
?|
C.![]() ��0.86
��0.86
D.��2=��|��2|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ涨�����Ϣ����˰�취�ǣ���Ϣ˰����Ϣ��20%������һ�궨�ڵ�����Ϊ2.25%����С��ȡ��һ�굽�ڵı�����Ϣʱ��������4.5Ԫ��Ϣ˰����С��һ��ǰ�������е�ǮΪ�� ��
A.1000Ԫ
B.900Ԫ
C.800Ԫ
D.700Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����B=90�㣬AB��DF��AB=4cm��BD=10cm����C���߶�BD��һ���㣬��E��ֱ��DF��һ���㣬��ʼ�ձ���AC��CE�� 
��1����ͼ1��˵������ACB=��CED��
��2����AC=CE������DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
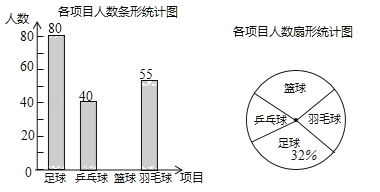
����Ŀ��ijѧУ����չ����������������������������������Ŀ������ƹ�����������ë��Ҫ��ÿλѧ��������ֻ��ѡ��һ�Ϊ�˽�ѡ������������Ŀ��ѧ�������������ȡ�˲���ѧ�����е��飬����ͨ�������õ����ݽ������������Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�ش����⣺
��1����λһ�������� ��ѧ����
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�ѡ��������Ŀ�������������ε�Բ�Ľǵ��� �ȣ�
��4������ѧУ��1500�ˣ�������Ƹ�ѧУѡ��������Ŀ��ѧ������Լ�� �ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����AOD=120�㣬AC=6������ABO���ܳ�Ϊ��������
A. 18 B. 15 C. 12 D. 9
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com