
 如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5.若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,我们把这种走法称为一次“移位”.
如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5.若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,我们把这种走法称为一次“移位”.分析 从编号为4的点开始走4段弧:4→5→1→2→3,即可得出结论;依次求出第2,3,4,5次的结合寻找规律,根据规律分析第2016次的编号即可.
解答 解:从编号为4的点开始走4段弧:4→5→1→2→3,所以第一次“移位”他到达编号为3的点;
第二次移位后:3→4→5→1,到编号为1的点;
第三次移位后:1→2,到编号为2的点;
第四次移位后:2→3→4,回到起点;
可以发现:他的位置以“3,1,2,4,”循环出现,
2016÷4=504,整除,所以第2016次移位后他的编号与第四次相同,到达编号为4的点;
故答案为:3,4.
点评 此题主要考查循环数列规律的探索与应用,根据已知求出部分数据找到循环周期是解题的关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{10}{3}$ | C. | $\frac{7}{10}$ | D. | $\frac{10}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
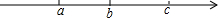 在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+a<0,则( )
在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+a<0,则( )| A. | b+c<0 | B. | |b|<|c| | C. | |a|>|b| | D. | abc<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| A | … | … | |||||
| B | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
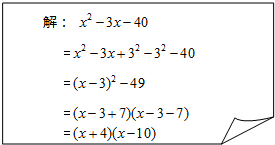
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{{(-2)}^2}}=2$ | B. | $\root{3}{{{{({-2})}^3}}}=-2$ | C. | $\sqrt{\frac{1}{2}}=\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{(-3)×({-2})}=\sqrt{-3}×\sqrt{-2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com