
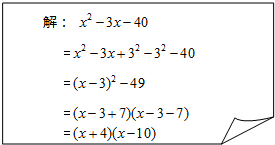
分析 (1)根据配方法,可得答案;
(2)根据配方法,可得平方差公式,再根据平方差公式,可得答案;
(3)根据交换律、结合率,可得完全平方公式,根据完全平方公式,可得答案.
解答 解:(1)x2+8x-1
=x2+8x+42-42-1
=(x+4)2-17;
(2)如图所示: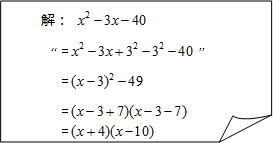
正确的解答过程:
x2-3x-40=x2-3x+($\frac{3}{2}$)2-($\frac{3}{2}$)2-40
=(x-$\frac{3}{2}$)2-$\frac{169}{4}$
=(x-$\frac{3}{2}$+$\frac{13}{2}$)(x-$\frac{3}{2}$-$\frac{13}{2}$)
=(x+5)(x-8);
(3)证明:x2+y2-2x-4y+16=(x2-2x+1)+(y2-4y+4)+11=(x-1)2+(y-2)2+11≥11,
故x,y取任何实数时,多项式x2+y2-2x-4y+16的值总为正数.
点评 本题考查了配方法,利用完全平方公式:a2±2ab+b2=(a±b)2配方是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5.若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,我们把这种走法称为一次“移位”.
如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5.若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,我们把这种走法称为一次“移位”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在等腰Rt△ABC中,∠ABC=90°,O是AC的中点,P,Q分别在AB,BC上(P,Q与A,B,C都不重合),OP⊥OQ,OS⊥AQ交AB于S.下列结论:①BQ=BS;②PA=QB;③S是PB的中点;④$\frac{CQ}{PS}$的值为定值.其中正确结论的个数是( )
如图,在等腰Rt△ABC中,∠ABC=90°,O是AC的中点,P,Q分别在AB,BC上(P,Q与A,B,C都不重合),OP⊥OQ,OS⊥AQ交AB于S.下列结论:①BQ=BS;②PA=QB;③S是PB的中点;④$\frac{CQ}{PS}$的值为定值.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
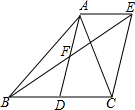 如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com