
【题目】若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( )
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为﹣4
D.抛物线与x轴的交点为(﹣1,0),(3,0)
【答案】C
【解析】解:∵抛物线过点(0,﹣3), ∴抛物线的解析式为:y=x2﹣2x﹣3.
A、抛物线的二次项系数为1>0,抛物线的开口向上,正确.
B、根据抛物线的对称轴x=﹣ ![]() =﹣
=﹣ ![]() =1,正确.
=1,正确.
C、由A知抛物线的开口向上,二次函数有最小值,当x=1时,y的最小值为﹣4,而不是最大值.故本选项错误.
D、当y=0时,有x2﹣2x﹣3=0,解得:x1=﹣1,x2=3,抛物线与x轴的交点坐标为(﹣1,0),(3,0).正确.
故选C.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,∠B=∠CAD. 
(1)求证:AC是⊙O的切线;
(2)若点E是 ![]() 的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面计算![]() +
+![]() +
+![]() +…+
+…+![]() 的过程,然后填空.
的过程,然后填空.
解:∵![]() =
=![]() (
(![]() -
-![]() ),
),![]() =
=![]() (
(![]() -
-![]() ),…,
),…,![]() =
=![]() (
(![]() -
-![]() ),
),
∴![]() +
+![]() +
+![]() +…+
+…+![]()
=![]() (
(![]() -
-![]() )+
)+![]() (
(![]() -
-![]() )+
)+![]() (
(![]() -
-![]() )+…+
)+…+![]() (
(![]() -
-![]() )
)
=![]() (
(![]() -
-![]() +
+![]() -
-![]() +
+![]() -
-![]() +…+
+…+![]() -
-![]() )
)
=![]() (
(![]() -
-![]() )
)
=![]() .
.
以上方法为裂项求和法,请参考以上做法完成:
(1)![]() +
+![]() =______;
=______;
(2)当![]() +
+![]() +
+![]() +…+x=
+…+x=![]() 时,最后一项x=______.
时,最后一项x=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=AC,∠BAC=45°,CD是△ABC的高,P是线段AC(不包括端点A,C)上一动点,以DP为一腰,D为直角顶点(D、P、E三点逆时针)作等腰直角△DPE,连接AE.

(1)如图1,点P在运动过程中,∠EAD=______,写出PC和AE的数量关系;
(2)如图2,连接BE.如果AB=4,CP=![]() ,求出此时BE的长.
,求出此时BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点,且DE∥BC,将△ADE沿DE翻折,与梯形BCED重叠的部分记作图形L.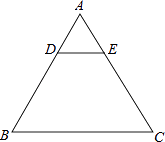
(1)求△ABC的面积;
(2)设AD=x,图形L的面积为y,求y关于x的函数解析式;
(3)已知图形L的顶点均在⊙O上,当图形L的面积最大时,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多美妙的性质,如关于线段比.面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题.请你利用重心的概念完成如下问题: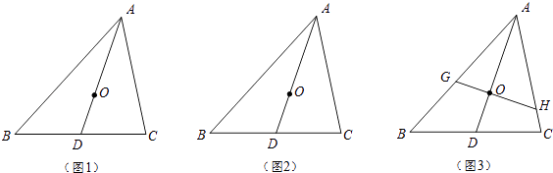
(1)若O是△ABC的重心(如图1),连结AO并延长交BC于D,证明: ![]() ;
;
(2)若AD是△ABC的一条中线(如图2),O是AD上一点,且满足 ![]() ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
(3)若O是△ABC的重心,过O的一条直线分别与AB、AC相交于G、H(均不与△ABC的顶点重合)(如图3),S四边形BCHG , S△AGH分别表示四边形BCHG和△AGH的面积,试探究 ![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com