【题目】如图，在等边△ABC中，AB=3，D、E分别是AB、AC上的点，且DE∥BC，将△ADE沿DE翻折，与梯形BCED重叠的部分记作图形L．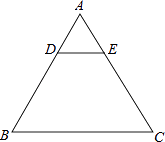

（1）求△ABC的面积；
（2）设AD=x，图形L的面积为y，求y关于x的函数解析式；
（3）已知图形L的顶点均在⊙O上，当图形L的面积最大时，求⊙O的面积．

参考答案：

【答案】
（1）

解：如图3，作AH⊥BC于H，

∴∠AHB=90°．

∵△ABC是等边三角形，

∴AB=BC=AC=3．

∵∠AHB=90°，

∴BH= BC=

在Rt△ABC中，由勾股定理，得

AH= ．

∴S△ABC= =


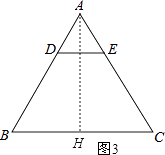
（2）

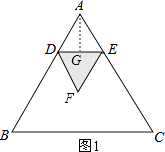
解：如图1，当0＜x≤1.5时，y=S△ADE．

作AG⊥DE于G，

∴∠AGD=90°，∠DAG=30°，

∴DG= x，AG= x，

∴y= = x2，

∵a= ＞0，开口向上，在对称轴的右侧y随x的增大而增大，

∴x=1.5时，y最大= ，

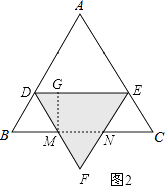
如图2，当1.5＜x＜3时，作MG⊥DE于G，

∵AD=x，

∴BD=DM=3﹣x，

∴DG= （3﹣x），MF=MN=2x﹣3，

∴MG= （3﹣x），

∴y= ，

=﹣ ；

综上所述，y关于x的函数解析式为：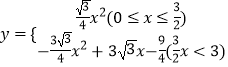


（3）

解：如图4，∵y=﹣ ；

∴y=﹣ （x2﹣4x）﹣ ，

y=﹣ （x﹣2）2+ ，

∵a=﹣ ＜0，开口向下，

∴x=2时，y最大= ，

∵ ＞ ，

∴y最大时，x=2，

∴DE=2，BD=DM=1．作FO⊥DE于O，连接MO，ME．

∴DO=OE=1，

∴DM=DO．

∵∠MDO=60°，

∴△MDO是等边三角形，

∴∠DMO=∠DOM=60°，MO=DO=1．

∴MO=OE，∠MOE=120°，

∴∠OME=30°，

∴∠DME=90°，

∴DE是直径，

S⊙O=π×12=π．


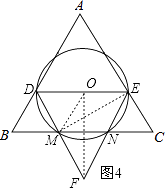
【解析】（1）作AH⊥BC于H，根据勾股定理就可以求出AH，由三角形的面积公式就可以求出其值；（2）如图1，当0＜x≤1.5时，由三角形的面积公式就可以表示出y与x之间的函数关系式，如图2，当1.5＜x＜3时，重叠部分的面积为梯形DMNE的面积，由梯形的面积公式就可以求出其关系式；（3）如图4，根据（2）的结论可以求出y的最大值从而求出x的值，作FO⊥DE于O，连接MO，ME，求得∠DME=90°，就可以求出⊙O的直径，由圆的面积公式就可以求出其值．
【考点精析】本题主要考查了翻折变换（折叠问题）的相关知识点，需要掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能正确解答此题．

关闭