
【题目】在等腰△ABC中,AB=AC,∠BAC=45°,CD是△ABC的高,P是线段AC(不包括端点A,C)上一动点,以DP为一腰,D为直角顶点(D、P、E三点逆时针)作等腰直角△DPE,连接AE.

(1)如图1,点P在运动过程中,∠EAD=______,写出PC和AE的数量关系;
(2)如图2,连接BE.如果AB=4,CP=![]() ,求出此时BE的长.
,求出此时BE的长.
【答案】(1)45°;PC=AE,(2)![]() .
.
【解析】
(1)根据全等三角形的性质即可得到结论;
(2)根据等腰直角三角形的性质得到∠DEP=∠DPE=45°,DE=DP.根据全等三角形的性质得到AE=PC=![]() ∠EAD=∠ACD=45°,过点E作EF⊥AB于F.根据勾股定理即可得到结论.
∠EAD=∠ACD=45°,过点E作EF⊥AB于F.根据勾股定理即可得到结论.
解:(1)PC=AE,
∵∠EDP=∠ADC=90°,
∴∠ADE+∠ADP=∠ADP+∠CDP=90°,
∴∠ADE=∠CDP,
在△ADE与△CDP中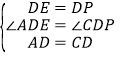 ,
,
∴△ADE≌△CDP(SAS),
∴∠EAD=∠PCD=45°,PC=AE;
故答案为:45°;
(2)如图,
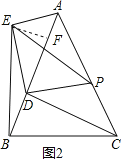
∵CD⊥AB,
∴∠ADC=90°.
∵∠BAC=45°,
∴AD=DC.
∵△DEP是等腰直角三角形,∠EDP=90°,
∴∠DEP=∠DPE=45°,DE=DP.
∵∠EDP=∠ADC=90°,
∴∠EDP-∠ADP=∠ADC-∠ADP.
∴∠EDA=∠PDC.
∴△EDA≌△PDC.(SAS),
∴AE=PC=![]() ∠EAD=∠ACD=45°,
∠EAD=∠ACD=45°,
过点E作EF⊥AB于F.
∴在Rt△AEF中,利用勾股定理,可得EF=AF=1,
∵AB=4,
∴BF=AB-AF=3.
∴BE=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=﹣ ![]() 的函数交于A(﹣2,b),B两点.
的函数交于A(﹣2,b),B两点. 
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为Rt△ABC的斜边,四边形ABGM,APQC,BCDE均为正方形,四边形RFHN是长方形,若BC=3,AC=4,则图中空白部分的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( )
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为﹣4
D.抛物线与x轴的交点为(﹣1,0),(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题.
为促进学生健康成长,切实提高学生健康水平,某校为各班用400元购进若干体育用品,接着又用450元购进第二批体育用品,已知第二批所购体育用品数是第一批所购体育用品数的1.5倍,且每件体育用品的进价比第一批的进价少5元,求第一批体育用品每件的进价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到![]() 的位置,
的位置,![]() ,
,![]() ,平移距离为6,则阴影部分面积为
,平移距离为6,则阴影部分面积为![]()
![]()

A. 24 B. 40 C. 42 D. 48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=ax+2by-1(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=a·0+2b·1-1=2b-1.已知T(1,-1)=-2,T(-3,2)=4.
(1)求a,b的值;
(2)利用(1)的结果化简求值:(a-b)2-(a+2b)·(a-2b)+2a(1+b).
查看答案和解析>>
科目:初中数学 来源: 题型:
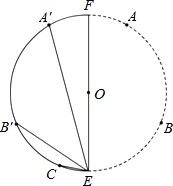
【题目】如图,A,B,C为⊙O上相邻的三个n等分点, ![]() ,点E在
,点E在 ![]() 上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°=
上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°= ![]() ,cos15°=sin75°=
,cos15°=sin75°= ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com