
ЁОЬтФПЁП2014ФъжЃжнЪаГЧеђУёгЊЦѓвЕОЭвЕШЫЪ§ЭЛЦЦ20ЭђЃЌЮЊСЫНтГЧеђУёгЊЦѓвЕдБЙЄУПдТЕФЪеШызДПіЃЌЭГМЦОжЖдШЋЪаГЧеђЦѓвЕУёгЊдБЙЄ2014ФъдТЦНОљЪеШыЫцЛњГщбљЕїВщЃЌНЋГщбљЕФЪ§ОнАДЁА2000дЊвдФкЁБЁЂЁА2000дЊЁЋ4000дЊЁБЁЂЁА4000дЊЁЋ6000дЊЁБКЭЁА6000дЊвдЩЯЁБЗжЮЊЫФзщЃЌНјааећРэЃЌЗжБ№гУAЃЌBЃЌCЃЌDБэЪОЃЌЕУЕНЯТСаСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
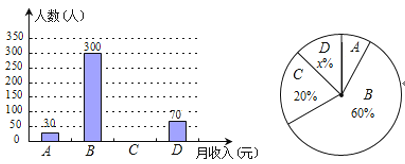
гЩЭМжаЫљИјГіЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮГщбљЕїВщЕФдБЙЄга_____ШЫЃЌдкЩШаЮЭГМЦЭМжаxЕФжЕЮЊ_____ЃЌБэЪОЁАдТЦНОљЪеШыдк2000дЊвдФкЁБЕФВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ_____ЃЛ
ЃЈ2ЃЉНЋВЛЭъећЕФЬѕаЮЭМВЙГфЭъећЃЌВЂЙРМЦЮвЪа2013ФъГЧеђУёгЊЦѓвЕ20ЭђдБЙЄжаЃЌУПдТЕФЪеШыдкЁА2000дЊЁЋ4000дЊЁБЕФдМЖрЩйШЫЃП
ЃЈ3ЃЉЭГМЦОжИљОнГщбљЪ§ОнМЦЫуЕУЕНЃЌ2013ФъЮвЪаГЧеђУёгЊЦѓвЕдБЙЄдТЦНОљЪеШыЮЊ4872дЊЃЌЧыФуНсКЯЩЯЪіЭГМЦЕФЪ§ОнЃЌЬИвЛЬИгУЦНОљЪ§ЗДгГдТЪеШыЧщПіЪЧЗёКЯРэЃП
ЁОД№АИЁПЃЈ1ЃЉ500ЃЛ14ЃЛ21.6ЁуЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉВЛКЯРэЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉгУBЕФШЫЪ§Г§вдЫљеМЕФАйЗжБШЃЌМЦЫуМДПЩЧѓГіБЛЕїВщЕФдБЙЄзмШЫЪ§ЃЌЧѓГіBЫљеМЕФАйЗжБШЕУЕНxЕФжЕЃЌдйЧѓГіAЫљеМЕФАйЗжБШЃЌШЛКѓГЫвд360ЁуМЦЫуМДПЩЕУНтЃЛ
ЃЈ2ЃЉЧѓГіCЕФШЫЪ§ЃЌШЛКѓВЙШЋЭГМЦЭММДПЩЃЌдйгУзмШЫЪ§ГЫвдBЫљеМЕФАйЗжБШМЦЫуМДПЩЕУНтЃЛ
ЃЈ3ЃЉВЛКЯРэЃЛвђЮЊ2000дЊЁЋ4000дЊЕФзюЖрЃЌеМ60%.
ЃЈ1ЃЉБОДЮГщбљЕїВщЕФдБЙЄШЫЪ§ЪЧЃК300ЁТ60%=500ЃЈШЫЃЉЃЌ
DЫљеМЕФАйЗжБШЪЧЃК70ЁТ500ЁС100%=14%ЃЌ
дђдкЩШаЮЭГМЦЭМжаxЕФжЕЮЊ14ЃЛ
ЁАдТЦНОљЪеШыдк2000дЊвдФкЁБЕФВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ360ЁуЁС![]() =21.6ЁуЃЌ
=21.6ЁуЃЌ
ЙЪД№АИЮЊ500ЃЌ14ЃЌ21.6ЁуЃЛ
ЃЈ2ЃЉCЕФШЫЪ§ЮЊЃК500ЁС20%=100ЃЌ
ВЙШЋЭГМЦЭМШчЭМЫљЪОЃЌ
ВЙШЋЭГМЦЭМШчЭМЫљЪОЃЛ
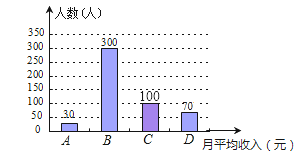
ЁА2000дЊЁЋ4000дЊЁБЕФдМЮЊЃК
20ЭђЁС60%=12ЭђЃЈШЫЃЉЃЛ
ЃЈ3ЃЉВЛКЯРэЃЛ
Ёп2000дЊЁЋ4000дЊЕФзюЖрЃЌеМ60%ЃЌ
ЁргУдТЦНОљЪеШыЮЊ4872дЊЗДгГдТЪеШыЧщПіВЛКЯРэЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
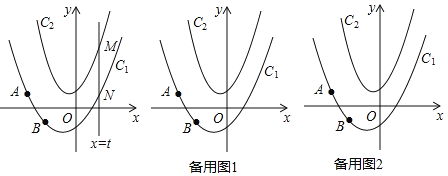
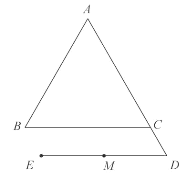
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпC1ЃКyЃНax2+bxЉ1ОЙ§ЕуAЃЈЉ2ЃЌ1ЃЉКЭЕуBЃЈЉ1ЃЌЉ1ЃЉЃЌХзЮяЯпC2ЃКyЃН2x2+x+1ЃЌЖЏжБЯпxЃНtгыХзЮяЯпC1НЛгкЕуNЃЌгыХзЮяЯпC2НЛгкЕуMЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпC1ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕБЁїAMNЪЧвдMNЮЊжБНЧБпЕФЕШбќжБНЧШ§НЧаЮЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЩшХзЮяЯпC1гыyжсНЛгкЕуPЃЌЕуMдкyжсгвВрЕФХзЮяЯпC2ЩЯЃЌСЌНгAMНЛyжсгкЕуKЃЌСЌНгKNЃЌдкЦНУцФкгавЛЕуQЃЌСЌНгKQКЭQNЃЌЕБKQЃН1ЧвЁЯKNQЃНЁЯBNPЪБЃЌЧыжБНгаДГіЕуQЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁЯACDЃН90ЁуЃЌACЃНDCЃЌMNЪЧЙ§ЕуAЕФжБЯпЃЌDBЁЭMNгкЕуBЃЎ
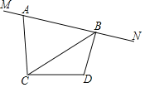
ЃЈ1ЃЉШчЭМЃЌЧѓжЄЃКBD+ABЃН![]() BCЃЛ
BCЃЛ
ЃЈ2ЃЉжБЯпMNШЦЕуAа§зЊЃЌдка§зЊЙ§ГЬжаЃЌЕБЁЯBCDЃН30ЁуЃЌBDЃН![]() ЪБЃЌЧѓBCЕФжЕЃЎ
ЪБЃЌЧѓBCЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЪЧаЁмПЩшМЦЕФЁАЙ§дВЭтвЛЕузївбжЊдВЕФЧаЯпЁБЕФГпЙцзїЭМЙ§ГЬЃЎ
вбжЊЃКЁбO МАЁбO ЭтвЛЕу PЃЎ
ЧѓзїЃКЁбO ЕФвЛЬѕЧаЯпЃЌЪЙетЬѕЧаЯпОЙ§Еу PЃЎ
зїЗЈЃКЂйСЌНг OPЃЌзї OP ЕФДЙжБЦНЗжЯп lЃЌНЛ OP гкЕу AЃЛ
Ђквд A ЮЊдВаФЃЌAO ЮЊАыОЖзїдВЃЌНЛЁбO гкЕу MЃЛ
ЂлзїжБЯп PMЃЌдђжБЯп PM МДЮЊЁбO ЕФЧаЯпЃЎ

ИљОнаЁмПЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌ
ЃЈ1ЃЉЪЙгУжБГпКЭдВЙцЃЌВЙШЋЭМаЮЃЛ(БЃСєзїЭМКлМЃ)
ЃЈ2ЃЉЭъГЩЯТУцЕФжЄУїЃК
жЄУїЃКСЌНг OMЃЌ
гЩзїЭМПЩжЊЃЌA ЮЊ OP жаЕуЃЌ
ЁрOP ЮЊЁбA жБОЖЃЌ
ЁрЁЯ ЃН90ЁуЃЈ ЃЉЃЈЬюЭЦРэЕФвРОнЃЉ
МД OMЁЭPMЃЎ
гжЁпЕу M дкЁбO ЩЯЃЌ
ЁрPM ЪЧЁбO ЕФЧаЯпЃЎЃЈ ЃЉЃЈЬюЭЦРэЕФвРОнЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШБп![]() жаЃЌDЮЊБпACЕФбгГЄЯпЩЯвЛЕуЃЈ
жаЃЌDЮЊБпACЕФбгГЄЯпЩЯвЛЕуЃЈ![]() ЃЉЃЌЦНвЦЯпЖЮBCЃЌЪЙЕуCвЦЖЏЕНЕуDЃЌЕУЕНЯпЖЮEDЃЌMЮЊEDЕФжаЕуЃЌЙ§ЕуMзїEDЕФДЙЯпЃЌНЛBCгкЕуFЃЌНЛACгкЕуGЃЎ
ЃЉЃЌЦНвЦЯпЖЮBCЃЌЪЙЕуCвЦЖЏЕНЕуDЃЌЕУЕНЯпЖЮEDЃЌMЮЊEDЕФжаЕуЃЌЙ§ЕуMзїEDЕФДЙЯпЃЌНЛBCгкЕуFЃЌНЛACгкЕуGЃЎ
ЃЈ1ЃЉвРЬтвтВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉСЌНгDFВЂбгГЄНЛABгкЕуHЃЌгУЕШЪНБэЪОЯпЖЮAHгыCGЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
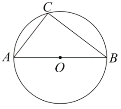
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌACЃЌBDЯрНЛгкЕуOЃЌЕуEЪЧOAЕФжаЕуЃЌСЌНгBEВЂбгГЄНЛADгкЕуFЃЌвбжЊSЁїAEF=4ЃЌдђЯТСаНсТлЃКЂй![]() ЃЛЂкSЁїBCE=36ЃЛЂлSЁїABE=12ЃЛЂмЁїAEFЁЋЁїACDЃЌЦфжавЛЖЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЃЛЂкSЁїBCE=36ЃЛЂлSЁїABE=12ЃЛЂмЁїAEFЁЋЁїACDЃЌЦфжавЛЖЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂкЂлЂм B. ЂйЂм C. ЂкЂлЂм D. ЂйЂкЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊЖўДЮКЏЪ§![]() (
(![]() ЮЊГЃЪ§ЃЌ
ЮЊГЃЪ§ЃЌ![]() )ЕФЭМЯѓЙ§Еу
)ЕФЭМЯѓЙ§Еу![]() КЭЕу
КЭЕу![]() ЃЌКЏЪ§ЭМЯѓзюЕЭЕу
ЃЌКЏЪ§ЭМЯѓзюЕЭЕу![]() ЕФзнзјБъЮЊ
ЕФзнзјБъЮЊ![]() ЃЎжБЯп
ЃЎжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]()
![]() ЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
![]() жБЯп
жБЯп![]() би
би![]() жсЯђгвЦНвЦЃЌЕУжБЯп
жсЯђгвЦНвЦЃЌЕУжБЯп![]() ЃЌ
ЃЌ![]() гыЯпЖЮ
гыЯпЖЮ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсЯТЗНЕФХзЮяЯпЯрНЛгкЕу
жсЯТЗНЕФХзЮяЯпЯрНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌАб
ЃЌАб![]() бижБЯп
бижБЯп![]() елЕўЃЌЕБЕу
елЕўЃЌЕБЕу![]() ЧЁКУТфдкХзЮяЯпЩЯЕу
ЧЁКУТфдкХзЮяЯпЩЯЕу![]() ЪБ(ЭМ
ЪБ(ЭМ![]() ЧѓжБЯп
ЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
![]() дк
дк![]() ЕФЬѕМўЯТЃЌ
ЕФЬѕМўЯТЃЌ![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌАб
ЃЌАб![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌPЮЊ
ЃЌPЮЊ![]() ЩЯЕФЖЏЕуЃЌЕБ
ЩЯЕФЖЏЕуЃЌЕБ![]() ЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЗћКЯЬѕМўЕФЕу
ЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЗћКЯЬѕМўЕФЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌЕу
ЕФжБОЖЃЌЕу![]() дк
дк![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() ЪЧ
ЪЧ![]() ЩЯвЛЖЏЕуЃЌЧвгыЕу
ЩЯвЛЖЏЕуЃЌЧвгыЕу![]() ЗжБ№ЮЛгкжБОЖ
ЗжБ№ЮЛгкжБОЖ![]() ЕФСНВрЃЌ
ЕФСНВрЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЛ
ЃЛ

ЃЈ1ЃЉЕБЕу![]() дЫЖЏЕНЪВУДЮЛжУЪБЃЌ
дЫЖЏЕНЪВУДЮЛжУЪБЃЌ![]() ЧЁКУЪЧ
ЧЁКУЪЧ![]() ЕФЧаЯпЃПЛГіЭМаЮВЂМгвдЫЕУїЃЎ
ЕФЧаЯпЃПЛГіЭМаЮВЂМгвдЫЕУїЃЎ
ЃЈ2ЃЉШєЕу![]() гыЕу
гыЕу![]() ЙигкжБОЖ
ЙигкжБОЖ![]() ЖдГЦЃЌЧв
ЖдГЦЃЌЧв![]() ЃЌЛГіЭМаЮЧѓДЫЪБ
ЃЌЛГіЭМаЮЧѓДЫЪБ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
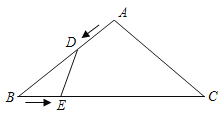
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЕШбќЁїABCжаЃЌABЃНACЃН10cmЃЌBCЃН16cmЃЎЕуDгЩЕуAГіЗЂбиABЗНЯђЯђЕуBдШЫйдЫЖЏЃЌЭЌЪБЕуEгЩЕуBГіЗЂбиBCЗНЯђЯђЕуCдШЫйдЫЖЏЃЌЫќУЧЕФЫйЖШОљЮЊ1cm/sЃЎСЌНгDEЃЌЩшдЫЖЏЪБМфЮЊtЃЈsЃЉЃЈ0ЃМtЃМ10ЃЉЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌЁїBDEЕФУцЛ§ЮЊ7.5cm2ЃЛ
ЃЈ2ЃЉдкЕуDЃЌEЕФдЫЖЏжаЃЌЪЧЗёДцдкЪБМфtЃЌЪЙЕУЁїBDEгыЁїABCЯрЫЦЃПШєДцдкЃЌЧыЧѓГіЖдгІЕФЪБМфtЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com