
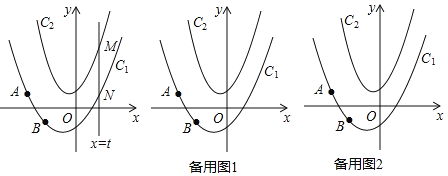
【题目】如图,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.
(1)求抛物线C1的表达式;
(2)当△AMN是以MN为直角边的等腰直角三角形时,求t的值;
(3)在(2)的条件下,设抛物线C1与y轴交于点P,点M在y轴右侧的抛物线C2上,连接AM交y轴于点K,连接KN,在平面内有一点Q,连接KQ和QN,当KQ=1且∠KNQ=∠BNP时,请直接写出点Q的坐标.
【答案】(1)y=x2+x﹣1;(2)t的值为1或0;(3)满足条件的Q点坐标为:(0,2)、(﹣1,3)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() ).
).
【解析】
(1)用待定系数法即可确定函数解析式;
(2)根据图形分∠ANM=90°和∠AMN=90°两种情况解答即可;
(3)根据题意画出满足条件图形,可以找到AN为△KNP对称轴,由对称性找到第一个满足条件Q,再通过延长和圆的对称性找到剩余三个点,利用勾股定理进行计算.
(1)∵抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1)
∴![]()
解得:![]()
∴抛物线C1:解析式为y=x2+x﹣1
(2)∵动直线x=t与抛物线C1交于点N,与抛物线C2交于点M
∴点N的纵坐标为t2+t﹣1,点M的纵坐标为2t2+t+1
∴MN=(2t2+t+1)﹣(t2+t﹣1)=t2+2
①当∠ANM=90°,AN=MN时,由已知N(t,t2+t﹣1),A(﹣2,1)
∴AN=t﹣(﹣2)=t+2
∵MN=t2+2
∴t2+2=t+2
∴t1=0(舍去),t2=1
∴t=1
②当∠AMN=90°,AM=MN时,由已知M(t,2t2+t+1),A(﹣2,1)
∴AM=t﹣(﹣2)=t+2,
∵MN=t2+2
∴t2+2=t+2
∴t1=0,t2=1(舍去)
∴t=0
故t的值为1或0;
(3)由(2)可知t=1时M位于y轴右侧,根据题意画出示意图如图:
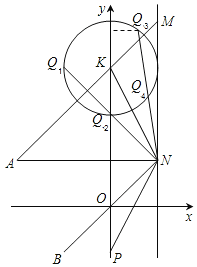
易得K(0,3),B、O、N三点共线
∵A(﹣2,1),N(1,1),P(0,﹣1)
∴点K、P关于直线AN对称
设半径为1的⊙K与y轴下方交点为Q2,则其坐标为(0,2)
∴Q2与点O关于直线AN对称
∴Q2是满足条件∠KNQ=∠BNP.
则NQ2延长线与⊙K交点Q1,Q1、Q2关于KN的对称点Q3、Q4也满足∠KNQ=∠BNP.
由图形易得Q1(﹣1,3)
设点Q3坐标为(m,n),由对称性可知Q3N=NQ1=BN=![]() ,
,
∵⊙K半径为1
∴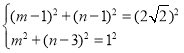
解得 或
或![]() .
.
同理,设点Q4坐标为(m,n),由对称性可知Q4N=NQ2=NO=![]() ,
,
∴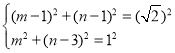
解得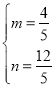 或
或![]() .
.
∴满足条件的Q点坐标为:(0,2)、(﹣1,3)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() ).
).


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
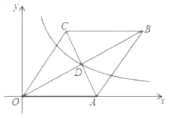
【题目】如图,在平面直角坐标系中,菱形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() 坐标为
坐标为![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .若将菱形
.若将菱形![]() 向左平移
向左平移![]() 个单位,使点
个单位,使点![]() 落在该反比例函数图象上,则
落在该反比例函数图象上,则![]() 的值为( ).
的值为( ).
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季试销售成本为每千克18元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元.经试销发现,销售量y(kg)与销售单价x(元/kg)符合一次函数关系,如图是y与x的函数关系图象.
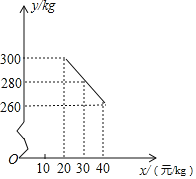
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小花在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小花身高1.5米,当她从点A跑动9![]() 米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10
米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10![]() 米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年郑州市城镇民营企业就业人数突破20万,为了解城镇民营企业员工每月的收入状况,统计局对全市城镇企业民营员工2014年月平均收入随机抽样调查,将抽样的数据按“2000元以内”、“2000元~4000元”、“4000元~6000元”和“6000元以上”分为四组,进行整理,分别用A,B,C,D表示,得到下列两幅不完整的统计图.
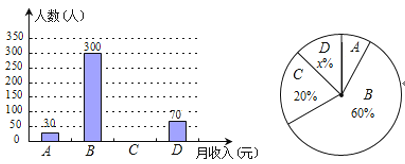
由图中所给出的信息解答下列问题:
(1)本次抽样调查的员工有_____人,在扇形统计图中x的值为_____,表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是_____;
(2)将不完整的条形图补充完整,并估计我市2013年城镇民营企业20万员工中,每月的收入在“2000元~4000元”的约多少人?
(3)统计局根据抽样数据计算得到,2013年我市城镇民营企业员工月平均收入为4872元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com